Regresión por cuantiles en R y SAS

Hace un tiempo, con la aburridora perspectiva de un largo viaje en metro hasta mi casa ensombreciendo mi futuro más inminente, decidí regalarme algún tipo de amena lectura. A tal fin, imprimí un articulillo que, bajo la perspectiva de SAS, me introducía a una técnica que se vino a mí como por azar. O, bajo otro punto de vista, una técnica que, también por azar, había esquivado hasta tal fecha un encontronazo con mi husmeadora curiosidad.

Y tengo que advertir a mis lectores que el tema no lo traigo acá sino porque me he topado con una aplicación (sobre la que no puedo comentar nada por estar bajo algo así como secreto de sumario) muy promisoria del mismo.

Se trata de la regresión por cuantiles.

Gran parte de lo que hay que saber sobre la cosa es:

1. Que la regresión “de toda la vida”, para cada x calcula el valor f(x) que viene a pasar por la media de la nube de puntos.
2. Que la vida no se agota en la media y que existen también otros estadísticos interesantes: la mediana, determinados cuantiles, etc.
3. Que dado un x sería práctico disponer de un método que nos proporcionase, por ejemplo, el primer cuartil de la distribución de los posibles valores de f(x).

Imaginemos una situación en que se manifiesta esta necesidad: una población de individuos con su edad y su renta. Uno puede estar interesado en calcular la renta media por edad… pero tal vez puede interesar a un estudio de, para cada edad, qué porcentaje de la población cae por debajo del umbral de la miseria (que se suele definir como un porcentaje de la mediana del ingreso).

Una opción es crear histogramas por rango de edades. Otra, utilizar regresión por cuantiles.

Veamos cómo se haría en R. Cargamos primero los paquetes necesarios para el ejemplo:

library(quantreg)
library(splines)

Cargamos el famoso conjunto de datos de Engel (no el Engel de siempre; otro), que relaciona el ingreso con el gasto en alimentación de decimonónicos obreros belgas:

data( engel )
head( engel )
income foodexp
1 420.16  255.84
2 541.41  310.96
3 901.16  485.68
4 639.08  403.00
5 750.88  495.56
6 945.80  633.80

Representamos los datos:

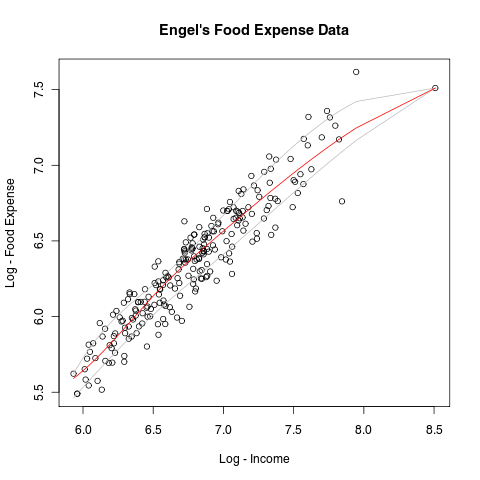
with( engel, plot( log( income ), log( foodexp ),
        xlab = "Log - Income",
        ylab = "Log - Food Expense",
        main = "Engel's Food Expense Data" ) )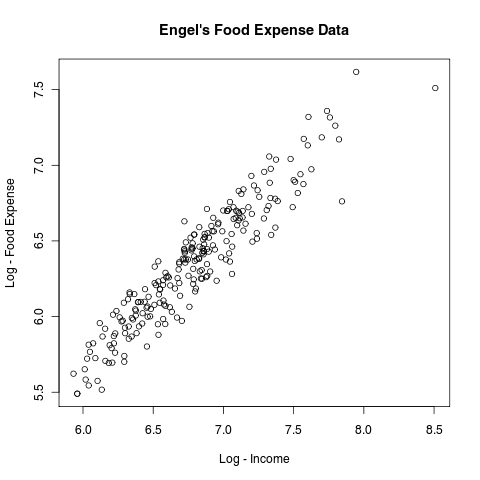

Y creamos una función auxiliar:

foo <- function( x, y, tau ){
    fit <- rq( y ~ bs( x, df=5 ), tau = tau )
    xx <- sort ( unique( x ) )
    data.frame( xx, predict( fit, newdata = data.frame( x = xx ) ) )
}

Nótese cómo en ella ajustamos un modelo de regresión por cuantiles, fit, usando la función rq del paquete quantreg y cómo también elegimos un regresor basado en splines, la función bs del paquete_ splines_. Sin incurrir en tanta pedantería, podíamos también haber especificado el modelo de la forma

    fit <- rq( y ~ x, tau = tau ),

dejándose el estudio del resultado de esta alternativa como ejercicio al lector más diligente.

El parámetro tau indica el cuantil que se desea estimar, que ha de ser, por lo tanto, un valor entre 0 y 1. Ahora podemos añadir a nuestro gráfico anterior las curvas estimación de los cuantiles 0,2; 0,5 y 0,8 de la distribución de la siguiente manera:

    with( engel, lines( foo( log( income ), log( foodexp) , 0.2 ),
       col="gray") )
    with( engel, lines( foo( log( income ), log( foodexp) , 0.8 ),
       col="gray") )
    with( engel, lines( foo( log( income ), log( foodexp) , 0.5 ),
       col="red" ) )

El lector interesado encontrará en internet dónde seguir instruyéndose y, además, ejemplos de gráficos espectaculares que pueden realizarse con quantreg, tiempo y buen gusto.