La red Asia

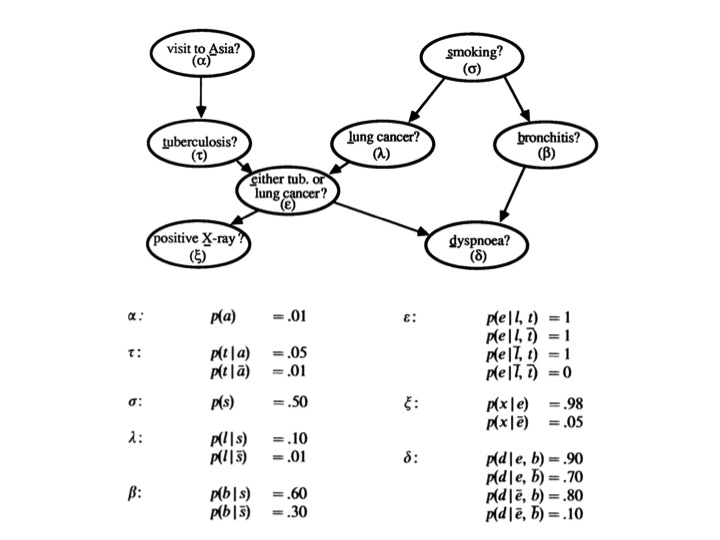
La red Asia es esto:

Es decir, una red bayesiana. Una red bayesiana clásica sobre la que los interesados podrán saber más leyendo lo que Lauritzen y Spiegelhalter dejaron escrito sobre ella en 1988.

Pero la idea básica es la siguiente:

• Los nodos superiores (visita a Asia, fumador) son variables observables sobre el comportamiento de unos pacientes.
• Los nodos inferiores (rayos X, disnea) son variables también observables, síntomas de esos pacientes.
• Los nodos centrales, los más importantes, no son observables: son diversas enfermedades que pudieran estar padeciendo los individuos en cuestión.

La pregunta que ayuda a resolver esta red bayesiana es la siguiente: conocidas (¡o no!) las variables observadas, ¿cuál es la probabilidad de que un paciente dado padezca alguna de las enfermedades (tuberculosis, bronquitis o cáncer de pulmón) correspondientes a los nodos centrales?

Nótense las relaciones de causalidad: fumar puede producir cáncer o bronquitis (pero no tuberculosis). Aparentemente, el haber visitado Asia (¡es un ejemplo ficticio!) incrementa la probabilidad de padecer tuberculosis. Tanto la tuberculosis como el cáncer pueden observarse (¡y confundirse!) con los rayos X. Etc.

Las probabilidades condicionales indican en qué medida unas causas inducen unos efectos. Por ejemplo, la probabilidad de que se observe algo en los rayos X cuando el paciente padece cáncer o tuberculosis es del 98%; y de que se observe algo cuando no es el caso, del 5%.

Y, ¿cómo analizamos esta red bayesiana? Podemos usar R, Google para ubicar esto y escribir:

library(gRain)

yn <- c("yes", "no")
a <- cptable(~ asia, values = c(1, 99), levels = yn)
t.a <- cptable(~ tub + asia, values = c(5, 95, 1, 99), levels = yn)
s <- cptable(~ smoke, values = c(5,5), levels = yn)
l.s <- cptable(~ lung + smoke, values = c(1, 9, 1, 99), levels = yn)
b.s <- cptable(~ bronc + smoke, values = c(6, 4, 3, 7), levels = yn)
x.e <- cptable(~ xray + either, values = c(98, 2, 5, 95), levels = yn)
d.be <- cptable(~ dysp + bronc + either, values = c(9, 1, 7, 3, 8, 2, 1, 9), levels = yn)
e.lt <- ortable(~ either + lung + tub, levels = yn)

plist <- compileCPT( list(a, t.a, s, l.s, b.s, e.lt, x.e, d.be))
BN <-grain(plist,smooth=0)

Con eso hemos definido y compilado la red bayesiana. Y entonces podemos hacer consultas sobre ella. Por ejemplo:

querygrain( BN, nodes = c("lung", "bronc"), type = "marginal")
# $lung
# lung
# yes    no
# 0.055 0.945
#
# $bronc
# bronc
# yes   no
# 0.45 0.55
querygrain( BN, nodes = c("lung", "bronc"), type = "joint")
# bronc
# lung     yes     no
# yes 0.0315 0.0235
# no  0.4185 0.5265

O de otra manera,

tmp <- setFinding(BN, nodes = c("asia", "dysp"), states = c("yes", "yes"))
querygrain(tmp, nodes = c("lung", "bronc"))
# $lung
# lung
# yes         no
# 0.09952515 0.90047485
#
# $bronc
# bronc
# yes        no
# 0.8114021 0.1885979
getFinding(tmp)
# Finding:
#   asia: yes
# dysp: yes
# Pr(Finding)= 0.004501375

La interpretación de los resultados anteriores queda como ejercicio a mis lectores así como el jugar con los parámetros para realizar otros cálculos sobre la red. No abundaré en eso.

Sí que lo haré para decir que era mi intención tirar del hilo de este tipo de modelos para encontrar indicios (no observables) de cierto tipo de comportamiento de clientes de un (valga la redundancia) cliente mío a partir de características sociodemográficas (nodos superiores) y comportamientos observados (nodos inferiores). Pero la cosa quedó en veráse.

(Nota: no sabía que esta red fuese tan popular y que fuese conocida por el nombre que titula la presente entrada; débole la info a alguien a quien debo como contraprestación, un café u dos).