Procesos puntuales: una primera aproximación
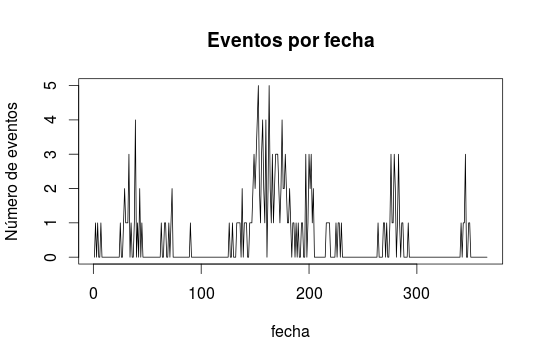
Tengo una serie de datos que se parecen a lo que cierta gente llama procesos puntuales y que se parecen a los que se introducen (muuuuy prolijamente) aquí. Gráficamente, tienen este aspecto:
Sobre un determinado periodo de tiempo (eje horizontal) suceden eventos y los cuento por fecha. Pero no suceden independientemente (como si generados por un proceso de Poisson) sino que tienden a agruparse: el que suceda un evento tiende a incrementar la probabilidad de que suceda otro poco después. El proceso, en una mala traducción, se autoexcita.
Sucede así con los terremotos (réplicas que se agrupan en el tiempo después de largos periodos de inactividad), las epidemias (¡el ébola!) y otros mundos menos catastróficos (paquetes que llegan a un enrutador).
En la entrada de hoy voy a mostrar código para, primero, simular este tipo de procesos:
# parámetros iniciales
mu <- 0.1
alfa <- 0.2
delta <- 5
# simulación
n <- 365
muestra <- rep(0L, n)
lambda <- function(i, muestra, mu, alfa, delta){
indices <- Filter(function(x) x < i & x > i - delta, 1:n)
cuantos <- sum(muestra[indices])
mu + alfa * cuantos
}
for (i in 1:length(muestra)){
muestra[i] <- rpois(1, lambda(i, muestra, mu, alfa, delta))
}
plot(muestra, type = "l", main = "Eventos por fecha",
xlab = "fecha", ylab = "Número de eventos")Primero he definido los parámetros que lo gobiernan: mu, alfa y delta. En un día i, el número de eventos que suceden se simula como rpois(1, lambda(i)), es decir, como una distribución de Poisson con un parámetro lambda que es igual a mu (una intensidad base) más alfa veces el número de eventos que suceden en los delta días anteriores.
(Nota: Exiten formulaciones alternativas usando decaimientos exponenciales que no discutiré aquí).
La pregunta es: dada una muestra de ese proceso, ¿es posible recuperar los parámetros de partida? Eso es importante porque tienen interpretaciones potencialmente útiles: ¿existe correlación entre los eventos? ¿Se retroalimentan? ¿Durante cuánto tiempo existe retroalimentación?
No es difícil convencerse de que
$$ P(x_1, \dots, x_n) = P(x_m, \dots, x_n | x_1, \dots, x_{m-1}) P(x_1, \dots, x_{m-1}) =$$
$$ P(x_m, \dots, x_n | \lambda(x_1, \dots, x_{m-1})) P(x_1, \dots, x_{m-1})$$
y de ahí que, finalmente,
$$ P(x_1, \dots, x_n) = \prod P(x_i | \lambda(x_1, \dots, x_{i-1}))$$
por lo que la verosimilitud tiene una forma no particularmente fea:
verosimilitud <- function(muestra, mu, alfa, delta){
lambdas <- sapply(1:length(muestra),
function(i) lambda(i, muestra, mu, alfa, delta))
log.pes <- mapply(dpois, muestra, lambdas, log = TRUE)
sum(log.pes)
}
res <- lapply(1:10,
function(cand.delta){
optim.ver <- function(x)
-verosimilitud(muestra,
x[1], x[2],
cand.delta)
res <- optim(c(0.5, 0.5), optim.ver,
lower = c(0.0001, 0.0001),
upper = c(1, 1), method = "L-BFGS-B")
c(res$par, res$value)
})
res <- data.frame(do.call(rbind, res))
colnames(res) <- c("mu", "alfa", "verosimilitud")
res$delta <- 1:nrow(res)
# mu alfa verosimilitud delta
# 1 0.51780828 0.50000000 381.3868 1
# 2 0.19511038 0.62320137 301.3827 2
# 3 0.12928483 0.37516357 287.8098 3
# 4 0.07450673 0.28537106 267.3672 4
# 5 0.06709883 0.21760683 262.1628 5
# 6 0.06248190 0.17586926 267.5603 6
# 7 0.05914818 0.14763133 268.1858 7
# 8 0.06136758 0.12592940 270.5051 8
# 9 0.06554786 0.10917939 275.5393 9
# 10 0.06987877 0.09611971 280.3062 10El código anterior construye la función de versosimilitud y la maximiza (de hecho, minimiza el opuesto de su logaritmo) y en la salida se puede observar cómo… bueeeno, efectivamente, se puede recuperar una versión desdibujada de los parámetros de entrada: delta igual a 5 (igual que el que genera el proceso), mu igual a 0.067 (vs 0.1) y alfa igual a 0.217 (vs 0.2).
Inestable y todo, los resultados son promisorios e igual llego a utilizarlos en algo más serio que la presente. A ver si saco tiempo estos días y planteo un par de extensiones y refinamientos que tengo en mente.