Colinealidad y posterioris

Estadística, R

En esta entrada voy a crear un conjunto de datos donde dos variables tienen una correlación muy alta, ajustar un modelo de regresión y obtener la siguiente representación de la distribución a posteriori de los coeficientes,

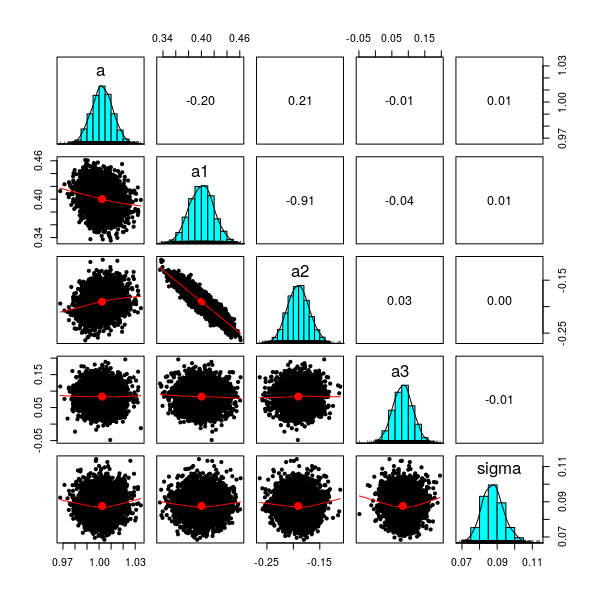
donde se aprecia el efecto de la correlación entre x1 y x2.

El código,

library(mvtnorm)
library(rstan)
library(psych)

n <- 100
corr_coef <- .9

x <- rmvnorm(n, c(0, 0),
  sigma = matrix(c(1, corr_coef, corr_coef, 1), 2, 2))
plot(x)

x1 <- x[,1]
x2 <- x[,2]
x3 <- runif(n) - 0.5

y <- 1 + .4 * x1 - .2 * x2 + .1 * x3 + rnorm(n, 0, .1)

summary(lm(y ~ x1 + x2 + x3))

stan_code <- "
data {
  int N;
  vector[N] y;
  vector[N] x1;
  vector[N] x2;
  vector[N] x3;
}
parameters {
  real a;
  real a1;
  real a2;
  real a3;
  real sigma;
}

model {
  a ~ cauchy(0,10);
  a1 ~ cauchy(0,2.5);
  a2 ~ cauchy(0,2.5);
  a3 ~ cauchy(0,2.5);

  y ~ normal(a + a1 * x1 + a2 * x2 + a3 * x3, sigma);
}"


datos_stan <- list(
    N = n,
    y = y,
    x1 = x1,
    x2 = x2,
    x3 = x3
)

fit2 <- stan(model_code = stan_code,
              data = datos_stan,
              iter = 10000, warmup = 2000,
              chains = 2, thin = 4)

res <- as.data.frame(fit2)
pairs.panels(res[, c("a", "a1", "a2", "a3", "sigma")])