¿Cómo obtener distribuciones uniformes dentro de triángulos?

Me entretuve el otro día en cómo muestrear uniformemente dentro de triángulos motivado por Randomly selecting points inside a triangle de John D. Cook.

Hay uno que se le ocurriría a cualquiera: el del rechazo. Se inserta el triángulo en un cuadrado y se seleccionan solo aquellos valores que caigan dentro del triángulo.

Hay otro, que no está en esa entrada, y que consiste en transformar el triángulo en un triángulo rectángulo mediante una transformación lineal que preserve el área (shear o cizallamiento), del tipo

$$(x,y) \rightarrow (x + a y, y)$$

para poder muestrear un triángulo rectángulo que siempre es más cómodo.

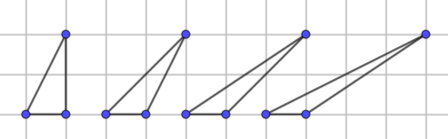
Luego, como John indica, es posible reciclar muestras rechazadas:

• Sin pérdida de generalidad, se puede suponer que el triángulo de interés es isósceles y que está contenido en el cuadrado unidad.
• Si se obtiene una muestra $(x, y)$ del cuadrado unidad e $y < x$, se acepta $(x,y)$.
• Pero si ocurre lo contrario, en lugar de descartar $(x, y)$, se puede elegir $(y, x)$.

Pero se puede pensar también en una solución baricéntrica: en efecto, si los vértices del triángulo son los puntos $A$, $B$ y $C$, entonces $a A + bB + cC$ son puntos del triángulo si $a$, $b$ y $c$ son números positivos que suman 1. Así que es fácil pensar en simular $a$, $b$ y $c$ con las restricciones anteriores para muestrear el triángulo. Es decir, hacer algo así como:

• Generar valores $a_0$, $b_0$ y $c_0$ de acuerdo con cierta distribución de probabilidad X.
• Después generar $a$, $b$ y $c$ como $a_0 / s$, $b_0 / s$ y $c_0 /s$ donde $s = a_0 + b_0 + c_0$.

Pero, como advierte Cook:

• Si se usa la distribución uniforme, el procedimiento falla.
• Si se usa la exponencial (da igual $\lambda$), funciona.
• Pero tampoco funciona con otras distribuciones al azar que se le ocurran a uno.

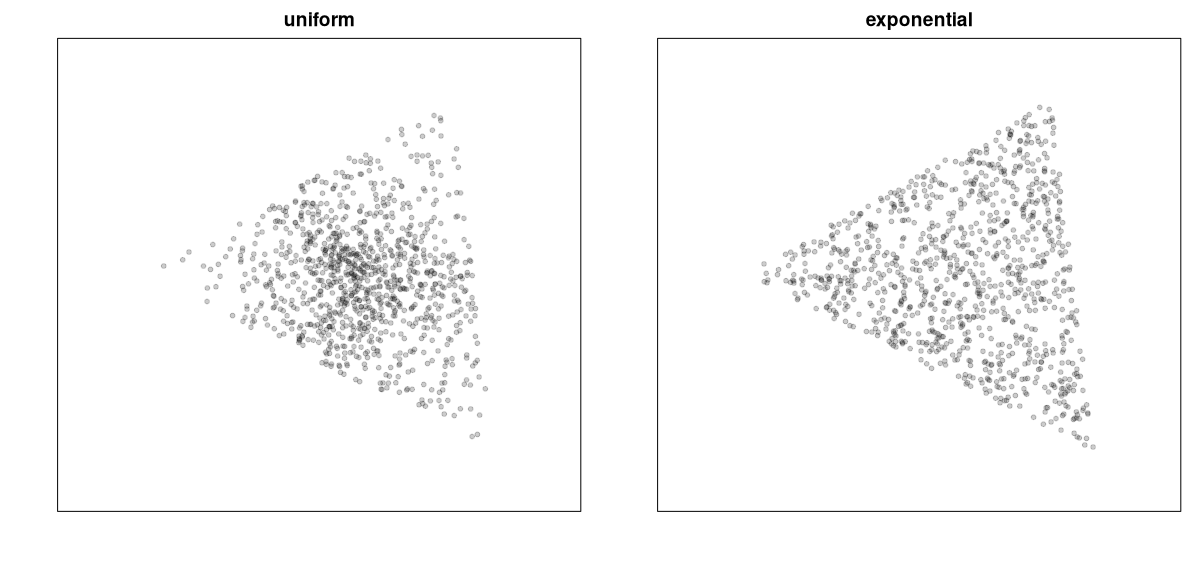
El motivo por el que esto funciona es que la distribución uniforme sobre un triángulo no es otra cosa que la distribución de Dirichlet con parámetros (1, 1, 1). El algoritmo habitual para muestrear una distribución de Dirichlet consiste en muestrear gammas y normalizar luego, con la salvedad de que para parámetros 1, esa gamma se reduce a una exponencial.

Coda

Por referencia, el código que he usado para generar el gráfico:

set.seed(1234)

n <- 1000

x0 <- c(1, 8, 9)
y0 <- c(5, 9, 1)


par(mfrow = c(1, 2),
    mar = c(3, 3, 2, 1),
    mgp = c(2, 0.5, 0))

plot(0, 0, type = "n", xlim = c(0, 10), ylim = c(0, 10),
     main = "uniform", xlab = "", ylab = "",
     xaxt = "n", yaxt = "n", asp = 1)

samples <- matrix(runif(n * 3), n, 3)
samples <- samples / rowSums(samples)

x <- samples %*% x0
y <- samples %*% y0

points(x, y, pch = 20, col = rgb(0, 0, 0, 0.2))

plot(0, 0, type = "n", xlim = c(0, 10), ylim = c(0, 10),
     main = "exponential", xlab = "", ylab = "",
     xaxt = "n", yaxt = "n", asp = 1)

samples <- matrix(rexp(n * 3, 1), n, 3)
samples <- samples / rowSums(samples)

x <- samples %*% x0
y <- samples %*% y0

points(x, y, pch = 20, col = rgb(0, 0, 0, 0.2))

par(mfrow = c(1, 1))