Capítulo 3 Probabilidades condicionales

TODO: el conocimiento es condicional; cómo especificar el contexto? O definiendo bien el espacio de probabilidad o usando el condicionamiento implícita o explícitamente.

En el capítulo anterior se introdujeron los conceptos de evento y de probabilidad asociada a un evento. Los eventos son conjuntos y las probabilides, unos números asociados a esos conjuntos —uno puede pensar, más o menos impropiamente, que se corresponden al tamaño o la medida de esos conjuntos— que obedecen ciertas reglas. En particular, que sean compatibles con la teoría de los conjuntos en el sentido, por ejemplo, de que si \(A \subset B\), entonces \(P(A) < P(B)\).

Ambos temas, conjuntos y medidas de dichos conjuntos, son genéricos y podría decirse que heredados de otras ramas de las matemáticas. Pero existe un concepto, el de las probabilidades condicionales, que es más propiamente probabilístico. De hecho, muchos dicen que no existe —o, más bien, que no tiene sentido práctico— la probabilidad del evento \(A\) como tal sino más bien la probabilidad de \(A\) condicionado a una serie de factores, a, en definitiva, un evento, muchas veces implícito, \(B\).

Del concepto de probabilidad condicional se derivan otros como el de independencia de eventos, las probabilidades marginales, conjuntas, etc. Y es posible, incluso, llegar a plantear —uno de los objetivos del capítulo— y demostrar el teorema de Bayes.

TODO: Un modelo es una probabilidad condicional.

3.1 Probabilidades condicionales

El concepto de probabilidad condicional está presente en el habla cotidiana. Son comunes, por ejemplo, expresiones del tipo:

Cuando llueve, la probabilidad de que se produzcan atascos es del 40%.

Si \(A\) es el evento “atascos”, la expresión anterior no significa que \(P(A) = .4\) dado que \(A\) incluye también el evento “atasco” en ausencia de lluvia.

Si \(B\) es el evento “lluvia”, la manera en que se representa la expresión anterior es

\[P(A \; | \; B ) = .4,\]

que se lee así: la probabilidad condicional de \(A\) dado \(B\) es del 40%.

Supongamos ahora que de cada 100 días, 10 llueve. Es decir, que \(P(B) = .1\). Entonces, de cada 100 días, 4 lloverá y habrá atasco. Es decir, \(P(A \cap B) = 0.04\). En general,

\[P(A \cup B) = P(A | B) \times P(B)\]

o, como se suele ver escrito por todas partes,

\[P(A | B) = \frac{P(A \cup B)}{P(B)}.\]

Frecuentemente, en lugar de usar \(P(A \cup B)\), por comodidad y a pesar de la ambigüedad que introduce la notación, se escribe \(P(A, B)\). En todo lo que sigue se usará una u otra notación indistintamente.

Hablar de probabilidades condicionales viene a ser equivalente a cambiar (o estrechar) el marco de referencia, el evento total. De hecho, por lo anterior, \(P(B | B) = 1\). Al condicionar por \(B\) ya no se tienen en cuenta todas las condiciones meteorológicas posibles sino solamente aquellas en que llueve.

De ahí que haya quienes niegan que tenga sentido hablar directamente de \(P(A)\) (véase, por ejemplo, (Keynes 1921)): siempre razonamos desde un marco de referencia muy concreto. Por ejemplo, al hablar de la probabilidad de que el Real Madrid gane su próximo partido, estaremos haciéndo, casi seguro, teniendo en cuenta si juega en casa, el rival, el estado actual de la plantilla, etc. Es decir, condicionado al evento que describe el contexto en el que se desarrollará el partido. En la práctica se omite la referencia a este evento contextual, mas no por ello deja de estar presente.

El concepto de la probabilidad condicional aparece en muchos más contextos, frecuentemente con denominaciones específicas. Por ejemplo, en epidemiología se distingue entre la tasa de mortalidad (o la probabilidad de morir a causa de una determinada enfermedad), que podríamos representar como \(P(M)\) y la tasa de letalidad, \(P(M\;|\;C)\), que es la probabilidad de morir condicionada a haber contraído la enfermedad. También se habla de tasa de paro (la probabilidad de estar desempleado) y, p.e., tasa de paro femenina, o la probabilidad de que una mujer se encuentre desempleada, que es la probabilidad de que una persona esté desempleada condicionada a que dicha persona es mujer (o \(P(D\;|\;M)\)).

Las probabilidades condicionales constituyen, podría decirse, el núcleo de la ciencia de datos. En un banco, por ejemplo, \(P(Y)\) podría representar la probabilidad de impago de una hipoteca y mostrarse, tal vez gráficamente, en un cuadro de mando tras calcularse mediante una consulta a la base de datos. También podrían mostrarse las probabilidades condicionales \(P(H \;|\;\text{provincia})\), posiblemente sobre un mapa. Porque, efectivamente, existe una relación conceptual entre las probabilidades condicionales y las operaciones basadas en la expresión group by de SQL. Trascendiendo ese mundo de indicadores simples, un modelo de los usados en ciencia de datos no es otra cosa que una estimación más o menos problemática de \(P(Y \;|\; X_1, \dots, X_n)\), la probabilidad de un impago (en este caso) dadas —o condicionadas a— una serie de eventos \(X_1, \dots, X_n\) que tratan de describir las circunstancias de un cliente concreto y que podrían incluir no solo su provincia, sino también su edad, sus ingresos, su historial crediticio, etc.

3.2 Independencia

La relación de independencia es tal vez la más simple (entre las no triviales, como por ejemplo, ser iguales o complementarios) que puede existir entre eventos. Dos eventos \(A\) y \(B\) son independientes cuando

\[P(A \cap B) = P(A) \times P(B).\]

Si se reescribe la definción anterior en términos de las probabilidades condicionales, queda de la forma

\[P(A | B) = P(A),\]

que es mucho más intuitiva. Quiere decir que el conocimiento de B no afecta para nada a la probabilidad de \(A\). Siguiendo con el ejemplo futbolístico, si \(A\) es el evento relacionado con la victoria en liga del equipo local y \(B\) es algún tipo de evento en las lunas de Saturno, es plausible que \(P(A | B) = P(B)\).

En la teoría de la probabilidad se pueden probar muchos teoremas relacionados con eventos independientes. Los eventos independientes interactúan todos entre sí de la misma manera, cualquiera que sea su naturaleza, y eso permite probar muchos resultados interesantes para los probabilistas. En capítulos sucesivos se mostrarán, de hecho, algunos de los más imporantes. Podría decirse que a los probabilistas les encantan los eventos (mutuamente) independientes.

Sin embargo, desde el punto de vista de la práctica de la ciencia de datos, la independencia es una propiedad más problemática: no solo es una propiedad cuasiquimérica —en el sentido de que realmente es difícil observar variables que sean estrictamente independientes—, sino que ni siquiera es deseable: para poder decir algo respecto a la probabilidad de un evento \(A\) a partir de otros eventos conocidos \(B_1, \dots, B_n\), interesa precisamente que los \(B_i\) no sean independientes de \(A\).

La ciencia de datos es posible gracias a una especie de discontinuidad causal (Bueno 2010). Si todos los fenómenos fuesen mutuamente interdependientes, no solo la ciencia de datos sino el conocimiento mismo sería imposible: para modelar cualquiera de ellos haría falta tener en cuenta todos los demás (incluido el proverbial aleteo de las mariposas del trópico). Lo mismo pasaría si nada guardase relación con nada: cada fenómeno sería una manifestación de un azar no sujeto a pauta alguna. Pero, generalmente, si interesa \(A\), se puede identificar un número razonable de fenómenos \(B_1, \dots, B_n\) relacionados con \(A\) que permiten acotar su comportamiento y, en la práctica, crear modelos.

3.3 Probabilidades conjuntas y marginales

Esta sección comienza describiendo un modelo probabilístico que se seguirá usando como referencia a lo largo del resto del capítulo. El model es el siguiente:

• En un determinado lugar, el 10% de los días llueve (y el 90% luce el sol).
• Cuando llueve, la probabilidad de que se produzcan atascos es del 40%.
• Cuando no llueve, la probabilidad de que se produzcan atascos es del 10%.

El modelo se puede representar gráficamentes así:

Gráficas como la anterior abundan en la literatura dedicada a construir representaciones relacionadas con conceptos probabilísticos que tienen como objetivo hacerlas más fáciles de interpretar y, de paso, tratar de evitar determinados errores en los que los humanos incurrimos con excesiva frecuencia (véase (Hoffrage et al. 2002)).

La probabilidad de que un día llueva y no haya atasco es \(0.06 = 0.1 \times 0.6\): el 10% de los días llueve y de ellos, el 60% no hay atascos. Análogamente, se puede calcular el resto de las combinaciones posibles y tabularlas así:

tiempo	atasco	probabilidad
sol	sí	0.09
sol	no	0.81
lluvia	sí	0.04
lluvia	no	0.06

Esta tabla representa la llamada probabilidad conjunta (de las variables tiempo y atasco). Nótese cómo la suma de las probabilidades es 1. Se ha construido a partir de las llamadas probabilidades marginales (del tiempo) y condicionales (de los atascos condicionados por el tiempo).

Por su parte, expresiones del tipo el 10% de los días llueve reciben el nombre de probabilidades marginales (por un motivo que luego quedará claro).

La tabla de probabilidades conjuntas también puede representarse de la forma equivalente

P(T,A)	atasco	no atasco
lluvia	0.04	0.06
sol	0.09	0.81

En ella, si se suman filas y columnas, se obtienen las probabilidades marginales

P(T,A)	atasco	no atasco	P(T)
lluvia	0.04	0.06	0.1
sol	0.09	0.81	0.9
P(A)	0.13	0.87	1

En este caso, solo consideramos dos variables, \(T\) y \(A\). En otras situaciones puede haber más variables y la probabilidad conjunta se representaría por medio de un (hiper)cubo de números (que seguirían sumando 1). En tales casos, las probabilidades marginales corresponderían a las sumas a lo largo de las distintas proyecciones. Por ejemplo, de tenerse las variables \(A\), \(B\) y \(C\), la probabilidad marginal \(P(A,B)\) se calcularía a partir de la conjunta así:

\[P(A,B) = \sum_i P(A,B, C = c_i).\]

Recuérdese cómo los valores de la tabla de probabilidades conjuntas, \(P(T,A)\), se han calculado más arriba así:

\[P(T,A) = P(A \; | \; T) P(T).\] Despejando, se obtiene la relación

\[ P(A \; | \; T) = \frac{P(T,A)}{P(T)} = \frac{P(T \cap A)}{P(T)}\]

que se usa a menudo como definición de la probabilidad condicional. Lo que dice la fórmula anterior es que la probabilidad \(P(A \; | \; \text{lluvia})\) se construye tomando la columna correspondiente de la tabla de probabilidades conjuntas y, como sus valores no suman la unidad, normalizando por su total, que es precisamente \(P(\text{lluvia})\).

En el fondo, todas las probabilidades son probabilidades condicionales; todas las probabilidades que usamos están, de un modo u otro, condicionadas a eventos implícitos: un aquí, un ahora,… Por ejemplo, las que a veces se llaman probabilidades subjetivas son aquellas que un, valga la redundancia, sujeto asigna a eventos condicionado por la información que se dispone acerca de ellos en un momento dado.

Para finalizar esta sección, merece la pena repasar cómo se ha calculado la probabilidad marginal de, por ejemplo, el atasco, \(A\). Se ha hecho en las tablas anteriores sumando verticalmente

\[P(A) = P(A, \text{lluvia}) + P(A, \text{sol}).\]

Pero, desarrollando la expresión anterior en términos de las probabilidades condicionales conocidas, se obtiene la expresión

\[P(A) = P(A \;|\; \text{lluvia}) P(\text{lluvia}) + P(A \;|\; \text{sol}) P(\text{sol}).\]

En general, si nos interesa calcular la probabilidad de un evento \(A\) y somos capaces de encontrar conjuntos disjuntos \(B_i\) tales que tanto \(P(B_i)\) como \(P(A \;|\; B_i)\) son conocidos, entonces podemos calcular

\[P(A) = \sum_i P(A \;|\; B_i) P(B_i),\]

expresión es conocida con el desafortunado nombre de teorema de la probabilidad total; divide y vencerás sería más adecuado.

Dado que \(\sum_i P(B_i) = 1\), \(P(A)\) es lo que se llama una combinación convexa de las probabilidades condicionales \(P(A \;|\; B_i)\).

Más adelante en el libro se discutirá el problema de estimar las probabilidades de eventos. El teorema de la probabilidad total es una herramienta que permite estimar la probabilidad de eventos complejos. De hecho, conceptos relacionados con este teorema son recurrentes en libros dedicados en exclusiva al tema de estimación de probabilidades y a la realización de predicciones, como (Tetlock and Gardner 2015). En este libro se describe la tarea de unos equipos que compiten estimando la probabilidad de eventos de significancia estratégica (p.e., ¿habrá un cambio de régimen en Corea del Norte en los próximos cinco años?). Una de las herramientas que usan estos pronosticadores es, precisamente, la de descomponer esos eventos en otros más simples (p.e., se reactivará la guerra con el vecino del sur; fallecerá el líder; el ejército protagonizará un golpe de estado; etc.), estimar sus probabilidades marginales y condicionales y recomponer usando el teorema de la probabilidad total la del evento de interés.

3.3.1 Independencia de variables aleatorias

En el ejemplo discutido en la sección anterior, por definición, el tráfico dependía del tiempo. Había una correlación —y podría argumentarse que una relación causal— entre los estados del tiempo y del tráfico; sin embargo, en muchas circunstancias encontramos eventos que podemos considerar independientes. Un ejemplo clásico, el ejemplo clásico, es el de los lanzamientos sucesivos de una moneda.

Si tiramos una moneda al aire, podemos suponer que \(P(H) = P(T) = 1/2\). Pero, ¿qué ocurre si la lanzamos al aire dos veces? Gráficamente,

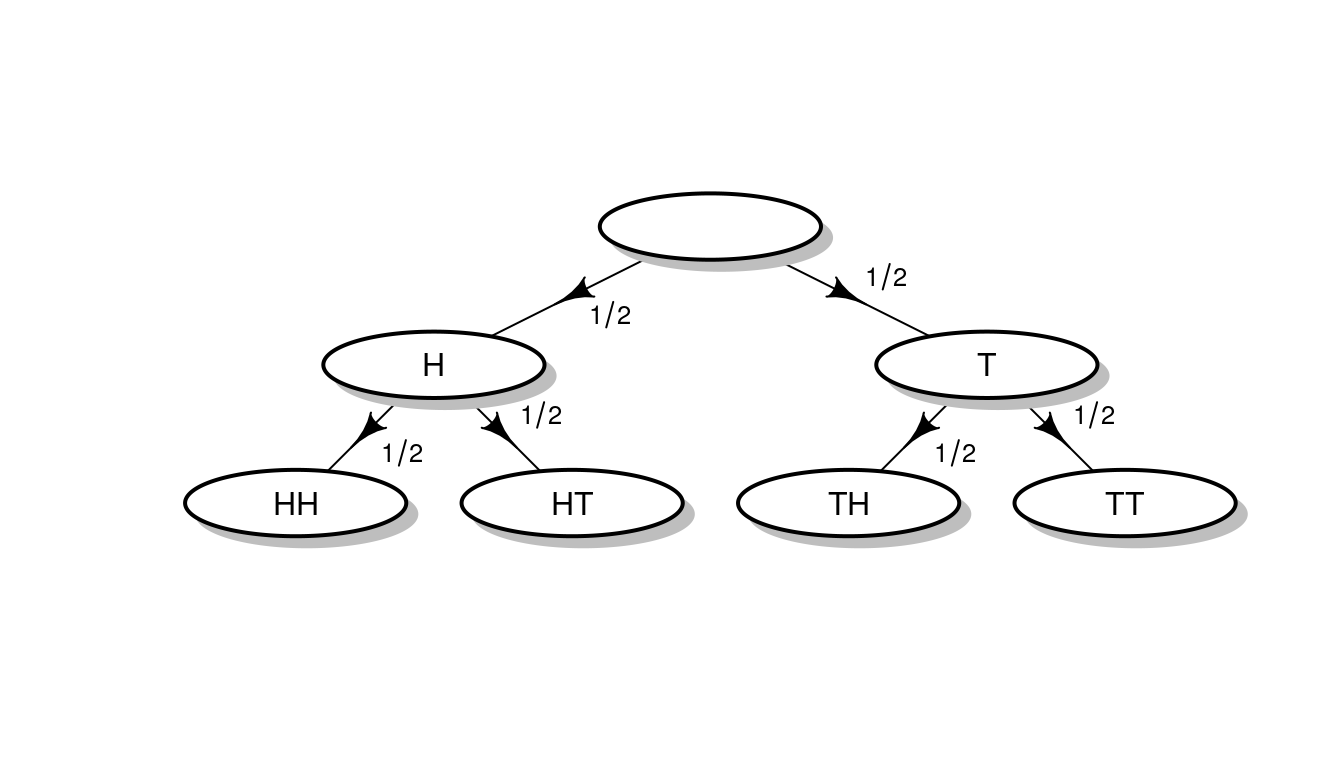
En el ejemplo original, como el estado del tiempo afecta al del tráfico,

\[P(\text{atasco} \; | \; \text{lluvia}) \neq P(\text{atasco} \; | \; \text{sol})\]

Pero en los lanzamientos de monedas,

\[P(H_2 \; | \; H_1) = P(H_2 \; | \; T_1)\]

y

\[P(T_2 \; | \; H_1) = P(T_2 \; | \; T_1).\]

Es decir, el resultado de la segunda tirada no está afectado por el de la primera y, de hecho,

\[P(H_2 \; | \; H_1) = P(H_2 \; | \; T_1) = P(H) = 1/2.\]

En general, se dice que dos eventos \(A\) y \(B\) son independientes, relación que frecuentemente se denota mediante \(A \perp B\), cuando \(P(A\;|\;B) = P(A)\). Cualitativamente, esto significa que conocer \(B\) no aporta información sobre \(A\). Y se dice que dos variables aleatorias \(X\) e \(Y\) son independientes cuando lo son los eventos que generan.

Si nos interesa explicar una variable aleatoria \(Y\) construyendo modelos basados en otras variables \(X_1, \dots, X_n\), como se ha dicho más arriba, interesa que \(Y\) no sea independiente de ninguna de las \(X_i\).

Pero existe otro modo en que consideraciones sobre la independencia de variables juegan un papel en la ciencia de datos. Tiene que ver con la relación entre las distintas observaciones \(y_i\). Frecuentemente, son independientes entre sí. Sin embargo, en muchos problemas interesantes no lo son. Por ejemplo:

• Si las \(y_i\) son observaciones ordenadas en el tiempo (p.e., temperaturas horarias).
• Si las \(y_i\) se refieren a ubicaciones (puesto que se correlacionan con otras \(y_j\) próximas).
• Si bloques de \(y_i\) se refieren a un mismo cliente, paciente o sujeto.

En esos casos, ignorar las relaciones de dependencia y asumir de facto la independencia de las observaciones conduce a modelos menos eficaces. Por eso existen modelos específicos para series temporales, modelos espaciales o los llamados modelos de medidas repetidas que se pueden aplicar, respectivamente, a los casos enumerados arriba. El quid de la cuestión reside en que asumir independencia cuando no la hay equivale a descartar información potencialmente útil.

Si \(A\) y \(B\) son independientes, su probabilidad conjunta es

P(A,B)	b0	b1	P(A)
a0	p1 * p3	p1 * p4	p1
a1	p2 * p3	p2 * p4	p2
P(B)	p3	p4	1

Precisamente porque

\[P(A,B) = P(A\; |\; B)P(B) = P(A)P(B).\]

De hecho, a menudo, se definen como independientes los eventos \(A\) y \(B\) cuando

\[P(A,B) = P(A)P(B).\]

Nosotros lo consideraremos una consecuencia de nuestra definición más que la definición en sí. De todos modos, la fórmula anterior proporciona un criterio rápido para determinar si dos variables aleatorias son o no independientes en algunos casos sencillos.

Las condiciones \(P(A,B) = P(A)P(B)\) o \(P(A|B) = P(A)\), que pueden usarse indistintamente como definiciones de independencia de eventos, no son realmente las que uno usa al enfrentarse a problemas reales. Frecuentemente no queda otra que remitirse al concepto intuitivo y cotidiano de independencia.

3.3.2 Regla de la cadena e independencia condicional

En el ejemplo considerado en esta sección hemos estudiado una situación en la que se interactuaban dos variables, \(T\) y \(A\) y hemos factorizado

\[P(T,A) = P(A \; | \; T) P(T)\]

En general, si tenemos \(A_1, A_2, A_3, A_4\), se cumple la llamada regla de la cadena:

\[P(A_1, A_2, A_3, A_4) = P(A_4 \; | \; A_1, A_2, A_3) P(A_3 \; | \; A_1, A_2) P(A_2 \; | \; A_1)P(A_1)\]

Esto se puede demostrar dibujando el gráfico correspondiente: se comienza con \(A_1\), se hace depender \(A_2\) de \(A_1\) y así sucesivamente. Obviamente, la factorización tiene sentido cuando se conocen las probabilidades condicionales implicadas.

Por ejemplo, de ser mutuamente independientes, la expresión anterior se reduce a

\[P(A_1, A_2, A_3, A_4) = P(A_1) P(A_2) P(A_3)P(A_4)\] Así ocurre al lanzar de monedas, donde, de hecho, se tiene, por ejemplo, que

\[P(HHTHT) = \frac{1}{2^5}.\]

La independencia mutua de variables aleatorias es una propiedad más fuerte que la de ser independientes dos a dos: exige que \(P(A_1 \cap \dots \cap A_n) = \prod P(A_i)\). De otra manera, la relación anterior no tendría que cumplirse necesariamente. Véase el siguiente ejercicio.

Ejercicio 3.1 Describe tres eventos cotidianos \(A\), \(B\) y \(C\) tales que \(A \perp B\), \(A \perp C\), pero que no se cumpla \(A \perp B \cap C\). Pista: puedes pensar en un evento \(A\) tal que \(B\) pueda tener un impacto positivo o negativo sobre su probabilidad de ocurrencia pero nulo en promedio y que ocurra lo mismo entre \(A\) y \(C\) pero que, sin embargo, \(A\) se vea afectado (p.e., negativamente) cuando ocurren simultáneamente \(B\) y \(C\).

El ejercicio anterior está estrechamente relacionado con un concepto fundamental de la ciencia de datos que es el de las interacciones entre variables: el efecto combinado de dos puede ser mayor (o menor) que el agregado de ambas por separado.

Ocurre además con frecuencia que se puede suponer, por ejemplo, que \(A_4\) no depende de \(A_1\) y \(A_2\), por lo que la expresión potencialmente compleja \(P(A_4|A_1, A_2, A_3)\) se reduce a la más manejable \(P(A_4|A_3)\). Sucede así, por ejemplo, con los llamados paseos aleatorios \(X_t\): una partícula, que en \(t = 0\) está en la posición \(0\) se mueve aleatoriamente cada segundo dando saltos equiprobables de tamaño \(-1\), \(0\) o \(1\).

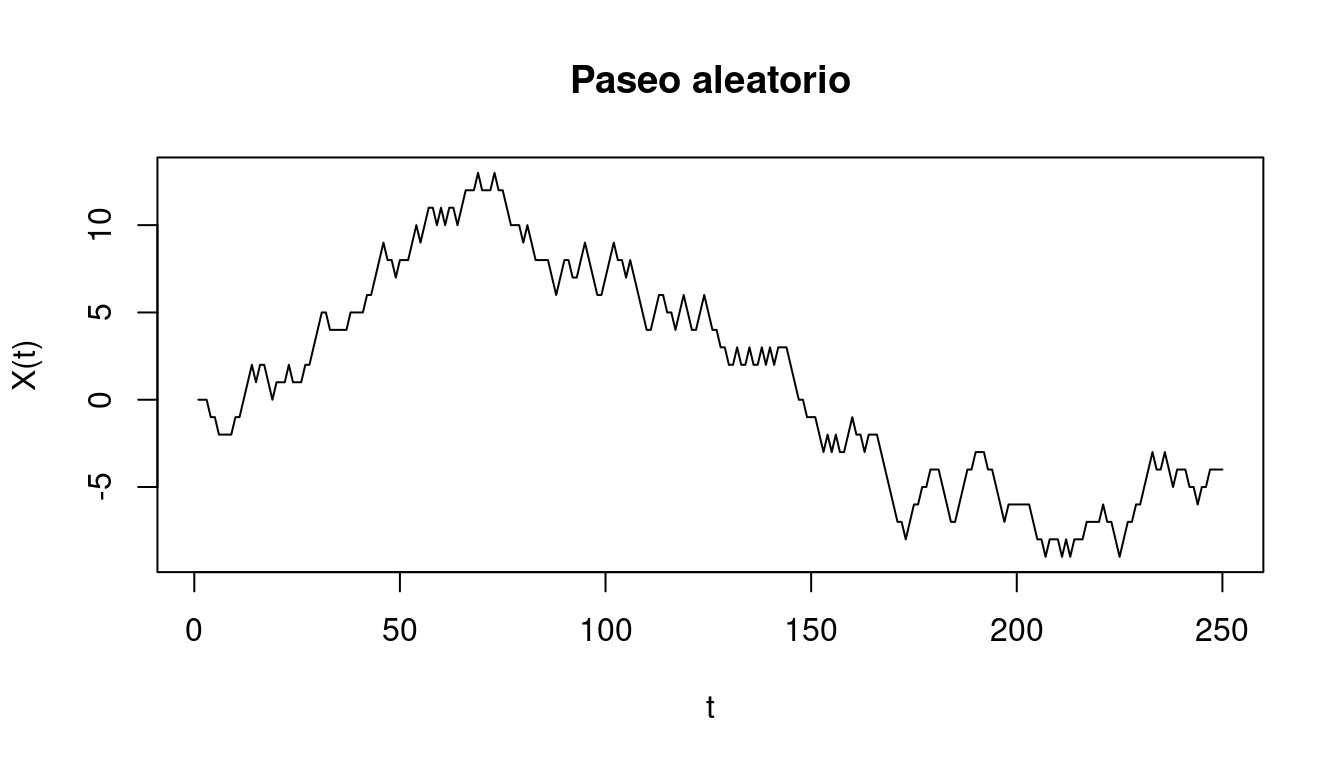
Entonces, \(X_T\) depende de \(X_t\) si \(t < T\), pero, conocido \(X_{T-1}\), \(X_T\) no depende de por dónde haya pasado previamente. Es decir, \(X_T\) no es independiente de \(X_t\), pero ambas variables aleatorias son condicionalmente independientes dado \(X_{T-1}\). La independencia condicional se representa así:

\[X_T \perp X_t \; | \; X_{T-1} \;\; \text{si} \; t < T-1.\]

En tales casos, la función de probabilidad conjunta puede factorizarse de la siguiente manera:

\[P(X_0, X_1, \dots, X_T) = P(X_0) \prod_{i = 1}^T P(X_i \; | \; X_{i-1}).\] Es una expresión un poco más compleja que la correspondiente a eventos independientes pero mucho más simple que la que se deduce de la regla de la cadena general. Precisamente porque se explotan las relaciones de independencia condicional.

Ejemplos como los de las caminatas aleatorias son campo minado para las probabilidades subjetivas de determinado tipo de sujetos siempre prestos a identificar relaciones entre \(X_T\) y secuencias de \(X_t\) previos tendencias o patrones de cualquier otro tipo.

El anterior es un ejemplo simple de las cadenas de Markov, que son secuencias de variables aleatorias en las que cada una de ellas es condicionalmente independiente de todas las que la preceden no inmediatamente condicionalmente en, precisamente, su predecesora inmediata.

El concepto de independencia condicional no es una mera construcción matemática sino un concepto usado implícitamente en muchas aplicaciones de la ciencia de datos. Por ejemplo, que un jubilado de Galicia y una señora de Cuenca hayan comprado un determinado producto, a pesar de la distancia, a pesar de no conocerse mutuamente, no tienen por qué ser eventos independientes: que el producto esté sujeto a una misma oferta, que ambos hayan visto el mismo anuncio,… Si el producto es, por ejemplo, turrón, el que lo haya comprado \(A\) aumenta las probabilidades de que lo haya comprado \(B\) porque, casi seguro, esos eventos están sucediendo en época de navidad. Sin embargo, al crear un modelo estamos aspirando a recoger sobre los sujetos involucrados una serie de variables tal que, a la vista de ellas, los comportamiento de los sujetos sean independientes. Es decir, estamos tratando de forzar relaciones de independencia condicional.

3.4 Teorema de Bayes

El modelo planteado al inicio de este capítulo partía del tiempo y, en función de él, definía la probabilidad de atasco. Pero es posible preguntarse cuál sería la probabilidad de que estuviese lloviendo a partir de la información del estado del tráfico. Es decir, calcular, por ejemplo, \(P(\text{lluvia} \; | \; \text{atasco})\) (y, en general, \(P(T \; | \; A)\)), i.e., invertir las probabilidades condicionales.

Contestar la pregunta anterior es sencillo porque, por definición,

\[P(T \; | \; A) = \frac{P(T,A)}{P(A)}\]

y tanto \(P(T,A)\) como \(P(A)\) son conocidos. No obstante, podemos obviar la referencia a la probabilidad conjunta desarrollando el numerador \(P(T,A)\) de la forma \(P(T,A) = P(A \; | \; T) P(T)\), con lo que

\[P(T \; | \; A) = \frac{P(A \; | \; T) P(T)}{P(A)}\]

La expresión anterior se conoce como teorema de Bayes.

En nuestro caso concreto,

\[P(\text{lluvia} \; | \; \text{atasco}) = \frac{P(\text{atasco} \; | \; \text{lluvia}) P(\text{lluvia})}{P(\text{atasco})} = \frac{0.4 \times 0.1}{0.13} \approx 0.31\]

En general, llueve el 10% de los días; no obstante, con la información adicional de que hay un atasco, la probabilidad estimada de lluvia crece hasta el 31%.

Este resultado es útil porque, con frecuencia, solo conocemos las probabilidades condicionales menos interesantes. Por ejemplo, nos pueden decir que la sensibilidad de un test para el covid-19 es del 85% y que su especificidad es del 98%. Eso quiere decir que

\[P(\text{test positivo}\;|\; \text{con covid-19}) = .85\]

y que

\[P(\text{test negativo}\;|\; \text{sin covid-19}) = .98.\]

Sin embargo, lo que nos preocupa realmente (por ejemplo, si nuestro test ha resultado positivo) es precisamente

\[P(\text{con covid-19} \;|\; \text{test positivo}),\]

por lo que es necesario utilizar el teorema de Bayes. La siguiente gráfica muestra la probabilidad que estemos realmente afectados por el covid-19 en caso de que nuestra prueba sea positiva:

Ejercicio 3.2 Utiliza el teorema de Bayes para escribir la función que se muestra en la figura anterior. Trata luego de implementarla en R para reproducir el gráfico anterior.

Como puede verse, esa probabilidad depende críticamente del nivel de prevalencia. De hecho, cuando esta es baja, casi todos los positivos son falsos: corresponden a ese 2% de positivos que se producen entre la población sana.

Es difícil infraestimar la importancia del teorema de Bayes en la ciencia de datos. Frecuentemente, uno puede construir expresiones del tipo \(P(D \;|\; \theta)\) que pueden representar lo que se llama un modelo generativo que describe cómo podrían generarse unos datos \(D\) de conocerse unos parámetros \(\theta\). Por ejemplo, \(\theta\) puede representar el CTR (click through rate) de una determinada keyword; por lo tanto, si se conoce \(\theta\) se puede estimar el número de clicks que puede generar en un periodo dado, es decir, \(D\).

Sin embargo, el problema fundamental al que se enfrenta el científico de datos es el inverso: determinar \(\theta\) a partir de los datos observados \(D\). Esto es, determinar \(P(\theta \;|\; D)\).

3.5 Causalidad

La causalidad es el santo grial del científico, incluido el de datos. Lo es porque proporciona mecanismos fiables para provocar efectos deseados. Los textos de teoría de la probabilidad tratan extensamente las relaciones de independencia, apenas las de dependencia y nunca las de causalidad. Esto último sucede porque la probabilidad, como se mostrará en esta sección, no tiene nada que decir acerca de la causalidad en el sentido de que es incapaz de distinguir las relaciones causales de las que no. Pero que sea así no es motivo para no decirlo claramente y desde el principio.

Eso sí, hay que tener en cuenta que la independencia y la causalidad determinista —es decir, aquella que postula que siempre que pasa A, pasa B— son los extremos de un arco de posibles relaciones entre variables aleatorias y, por supuesto, los fenómenos que estas representan.

Desafortunadamente, es muy tentador atribuir mecanismos causales a relaciones de dependencia \(P(A \; | \; B) \ne P(A)\). Así, por ejemplo, al decir que \(P(A \; | \; B) > P(A)\), muchos podrían pensar que \(B\) facilita, fomenta o provoca \(A\). En efecto, hay casos conspicuos en que sucede así: piénsese en el caso en el que \(A\) y \(B\) son determinados tipos de cánceres y el tabaquismo, respectivamente. Sin embargo, esta no es la regla general. Hay que advertir además, que esta problemática (y frecuentemente falsa) atribución de causalidad se realiza tanto al discutir probabilidades condicionales directamente o a través de otras manifestaciones de las probabilidades condicionales más habituales, como por ejemplo, la correlación —que veremos más adelante— o los modelos estadísticos construidos sobre datos observacionales.

El siguiente ejemplo ilustra la cuesión. Se puede argumentar causalmente que la lluvia propicia los atascos, por lo que tiene sentido plantear que \(P(\text{atasco} \; | \; \text{lluvia}) > P(\text{atasco})\) como en el ejemplo discutido en esta sección. Sin embargo, usando el teorema de Bayes, llegamos a la conclusión de que \(P(\text{lluvia} \; | \; \text{atasco}) \ne P(\text{lluvia})\) sin que por ello sea lícito argumentar que los atascos tienen un efecto sobre la meteorología (al menos, en el cortísimo plazo). Si \(P(A \; | \; B) \ne P(A)\) tuviese una lectura del tipo \(B\) causa \(A\), como también podríamos derivar \(P(B \; | \; A) \ne P(A)\), se obtendría un absurdo.

Ejercicio 3.3 Expresa en términos de probabilidades condicionales la siguiente proposición: si conocer \(A\) aumenta la probabilidad de \(B\), entonces el que ocurra \(B\) aumenta la probabilidad de que ocurra \(A\). Además, busca 2 o 3 ejemplos concretos en los que la proposición anterior resulte intuitiva. Finalmente, demuéstrala.

Los neutrinos son unas partículas muy sutiles que prácticamente no interaccionan con la materia y la atraviesan sin dejar apenas rastro. Hacen falta instrumentos muy complejos y costosos para detectar su presencia. De la misma manera, la causalidad atraviesa tanto la teoría de la probabilidad como gran parte (en particular, toda la que se presenta en este libro) de la estadística² sin que puedan aprehenderla. En realidad, las probabilidades condicionales y los modelos estadísticos (que, como se verá, están muy relacionados con las probabilidades condicionales), predican sobre flujos de información. Así, el que llueva proporciona información sobre el posible estado de las calles; pero, a la inversa, el estado del tráfico puede proporcionar información sobre las condiciones meteorológicas. Conocer las causas modifica nuestra percepción de la probabilidad de los efectos; pero a la inversa, la observación de unos efectos proporciona información sobre la plausibilidad de sus posibles causas.

Nótese además cómo la discusión anterior aplica a parejas de variables entre las que existen relaciones de causalidad como en el siguiente diagrama.

Sin embargo, es posible (y, de hecho, es frecuente) encontrar otras configuraciones causales, como estas:

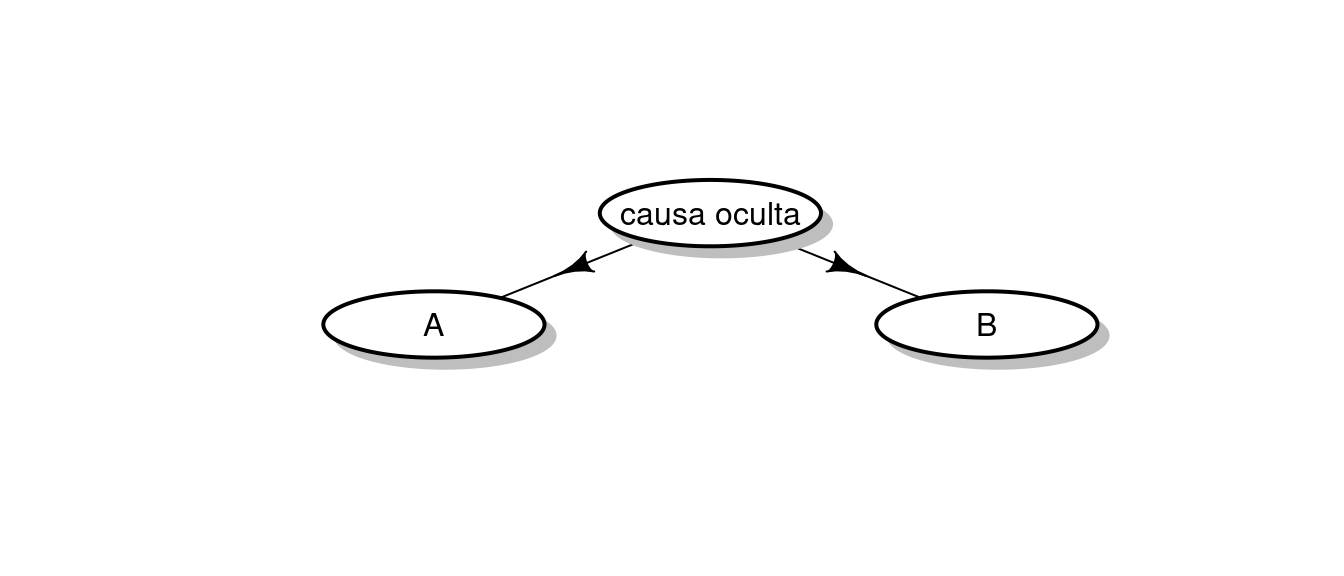
En esos casos también ocurre que \(P(A \; | \; B) \ne P(A)\) porque, de nuevo, conocer B revela información sobre A. El ejemplo clásico que suele citarse es el de que durante muchos años, la industria del tabaco argumentó que podría ser posible que existiese alguna causa biológica que tuviese dos efectos: propensión a la adicción al tabaco y propensión a desarrollar determinados tipos de tumor. Pero cuando uno lee artículos en los que se vincula el nivel de contaminación del aire con el número de hospitalizaciones por determinadas enfermedades respiratorias argumentando que ambos indicadores se mueven en paralelo a lo largo del año, uno siempre puede plantearse si ambas tienen una causa común llamada invierno.

Ni que decir tiene que en situaciones reales las relaciones entre variables pueden ser mucho más complejas y que prácticamente ningún fenómeno, particularmente fuera de los campos de la física o la ingeniería, es monocausal.

3.6 Apéndice: SamIam

SamIam (Automated Reasoning Group at UCLA 2010) es una herramienta para modelar y razonar sobre redes bayesianas desarrollado en la Universidad de California en Los Ángeles (UCLA). Permite representar relaciones de dependencia entre variables aleatorias discretas a través de una interfaz gráfica y, luego, realizar cálculos sobre ellas.

SamIam se puede descargar libremente y los tutoriales en línea ilustran con detalle los dos tipos de operaciones básicas en su manejo:

• Cómo crear variables aleatorias y especificar las probabilidades marginales y condicionales que definen su estructura probabilística.
• Cómo realizar inferencias sobre la red (p.e., marcar un nodo que representa la variable aleatoria que indica el color de una bola extraída de una urna como blanco para ver cómo varían el resto de las probabilidades).

3.7 Bibliografía razonada

Manuales de teoría de probabilidad al uso tales como (Gnedenko 1998) o (Gallier 2014) proporcionan una introducción tal vez más extensa, detallada y formal al asunto tratado en este capítulo.

La discusión sobre la causalidad ha sido extremadamente sobria, hasta el extremo en incurrir en sobresimplificaciones que aquí se quieren enmendar a golpe de bibliografía. Los humanos parecemos programados para preguntarnos por el por qué de las cosas (aunque existen opiniones discrepantes como (Anderson, C. 2008)). La ciencia de datos pretende e intenta comprender el mundo que nos rodea a través de los datos y, sin embargo, el libro argumenta que la causalidad es inasequible tanto para la teoría de la probabilidad como para gran parte de lo que conocemos como estadística. Ocurre que la manera más segura para poder establecer relaciones causales no tiene que ver tanto con el análisis de los datos sino sobre la manera en que estos se recogen. De cómo organizar la recogida de datos para poder descubrir relaciones causales se encarga la disciplina del diseño de experimentos (Design of experiments 2020), que tiene manifestaciones, límites, procedimientos e incluso recibe nombres distintos según el ámbito de aplicación: ingeniería, medicina, sicología, economía, etc. (véase (Sampedro 1983)).

Desafortunadamente, existe también la urgencia por establecer relaciones causales a partir de datos observacionales, es decir, recogidos sin los protocolos que establece el diseño experimental. Esto ocurre, por ejemplo, en epidemiología, cuando se detecta un brote infeccioso y urge identificar los fabricantes y los lotes de comida que puedan haberlo causado (puede consultarse, por ejemplo, (2011 Germany E. coli outbreak 2020)). La falta de datos experimentales —e incluso la imposibilidad práctica misma de obtenerlos— obliga en ocasiones a intentar obtener conclusiones causales a partir de datos observacionales (véase (Gil Bellosta, Carlos J. 2011)). De una manera más formal, los trabajos de Pearl (y, en particular, (Pearl 2009), cuyo último capítulo es una excelente introducción histórica al problema de la causalidad) tratan el mismo problema: la determinación de relaciones causales cuando no se cuenta con datos experimentales.

Aunque, en el fondo, ¿qué consecuencias tiene dar por buena una relación causal que, en el fondo, no existe? El autor está tentado, llegado a este punto, podría hilar anécdotas recopiladas a lo largo de su experiencia laboral, pero en términos de categorías recomienda reflexionar sobre (Goodhart’s law 2020) y (Lucas critique 2020).

Finalmente, existe mucho material publicado sobre el teorema de Bayes y sus aplicaciones, algo sobre lo que se volverá en capítulos posteriores de este libro. Mucha de esta literatura es técnica o semitécnica, aunque cabe mencionar un par de libros ((Mcgrayne 2012) y (Silver 2012)) que no solo tratan la cuestión desde un punto de vista divulgativo e intuitivo sino que, al parecer de muchos y sobre todo en el segundo caso, lo consiguen.

3.8 Ejercicios

Ejercicio 3.4 En una empresa de seguros los clientes son hombres (60%) y mujeres (40%). Tienen coches de color rojo, gris u otros. Para los hombres, el porcentaje de coches grises y de otros colores es igual, pero el de coches rojos es el doble que los anteriores. Para las mujeres, sucede lo mismo, solo que el porcentaje de coches rojos es la mitad que los otros.

La tasa de siniestros (si un cliente tuvo un siniestros en un año dado) es del 10% para hombres y mujeres independientemente del color del coche con las siguientes excepciones:

• Es el doble para los hombres que conducen coches rojos.
• Es la mitad para las mujeres que conducen coches grises.

Dibuja la gráfica que describe las probabilidades anteriores.

Ejercicio 3.5 Construye la tabla de probabilidad conjunta asociada a las variables aleatorias descritas en el ejercicio anterior.

Ejercicio 3.6

• Calcula la probabilidad marginal de los colores de los coches.
• Calcula la probabilidad marginal de colores y siniestralidad (una tabla que contenga la probabilidad de que un coche de un determinado color tenga o no un accidente).

Ejercicio 3.7 Calcula la probabilidad de siniestro según el color del vehículo.

Ejercicio 3.8 De ocurrir un siniestro, calcula la probabilidad de que la afectada sea mujer.

Ejercicio 3.9 Usa SamIam para modelar el problema de la empresa de seguros y úsalo para resolver los ejercicios relacionados con el teorema de Bayes planteados más arriba.

Ejercicio 3.10 Hay tres urnas que contienen, respectivamente, 2, 3 y 5 bolas blancas y 2, 4 y 1 bolas negras. Alguien elige una urna al azar y extrae una bola, que resulta ser blanca. ¿Cuál es la probabilidad de que la urna de la que se ha extraído la bola sea la primera?

Ejercicio 3.11 Recalcula la probabilidad si se extrae una bola más y resulta ser negra.

Ejercicio 3.12 Modela el ejercicio anterior usando SamIan y resuélvelo con él.

Ejercicio 3.13 Prueba que si \(A \perp B\), entonces \(A \perp \bar{B}\) y \(\bar{A} \perp \bar{B}\).

Ejercicio 3.14 Si el saber que Messi está lesionado incrementa las probabilidad de que el Barcelona pierda el próximo partido, ¿qué pasa si se sabe que Messi no está lesionado? En general, si A aumenta la probabilidades de B, ¿qué pasa con \(P(B)\) si se sabe que no ocurre A? ¿Qué tiene que ver lo anterior con la descomposición (pruébala) \(P(B) = P(B \; | \; A) P(A) + P(B \; | \; \bar{A}) P(\bar{A})\)?

Ejercicio 3.15 Calcula la probabilidad de obtener 3 caras en 4 lanzamientos de monedas.

Ejercicio 3.16

• ¿Cuál es la probabilidad de sacar un 2 o un 6 tirando un dado? (Usa los axiomas de probabilidad)
• ¿Cuál es la probabilidad de sumar 7 puntos en dos tiradas de dados?
• ¿Cuál es la probabilidad de no sacar un 1 tirando un dado?
• ¿Cuál es la probabilidad de no sacar ningún 1 después de tirar n dados? (Usa la independencia)

Ejercicio 3.17 ¿Qué es más probable, sacar un as tirando cuatro dados (una vez), o sacar dos ases en alguna de 24 tiradas de dos dados? (Es el problema del caballero de Méré)

Ejercicio 3.18 Demostrar que \(P(A\;|\; B, A \cup B) \le P(A ;|\; A \cup B)\), desigualdad conocida como la paradoja de Berkson.

Referencias

2011 Germany E. coli outbreak. 2020. “2011 Germany E. Coli O104:H4 Outbreak — Wikipedia, the Free Encyclopedia.” https://en.wikipedia.org/wiki/2011_Germany_E._coli_O104:H4_outbreak.

Anderson, C. 2008. “The End of Theory: The Data Deluge Makes the Scientific Method Obsolete.” https://www.wired.com/2008/06/pb-theory/.

Automated Reasoning Group at UCLA. 2010. “Samian: Sensitivity Analysis, Modelling, Inference and More.” http://reasoning.cs.ucla.edu/samiam/.

Bueno, G. 2010. “Symploké.” https://www.youtube.com/watch?v=fML2Ysy6l6s.

Design of experiments. 2020. “Design of Experiments — Wikipedia, the Free Encyclopedia.” https://en.wikipedia.org/wiki/Design_of_experiments.

Gallier, J. 2014. An Introduction to Discrete Probability. http://www.cis.upenn.edu/~jean/proba.pdf.

Gil Bellosta, Carlos J. 2011. “Causalidad O Asociación: Indicios de La Primera.” https://www.datanalytics.com/2011/04/20/causalidad-o-asociacion-indicios-de-la-primera/.

Gnedenko, B. V. 1998. Theory of Probability. Taylor & Francis.

Goodhart’s law. 2020. “Goodhart’s Law — Wikipedia, the Free Encyclopedia.” https://en.wikipedia.org/wiki/Goodhart%27s_law.

Hoffrage, Ulrich, Gerd Gigerenzer, Stefan Krauss, and Laura Martignon. 2002. “Representation Facilitates Reasoning: What Natural Frequencies Are and What They Are Not.” Cognition 84 (August): 343–52. https://doi.org/10.1016/S0010-0277(02)00050-1.

Keynes, John Maynard. 1921. A Treatise on Probability. Macmillan & Co.

Lucas critique. 2020. “Lucas Critique — Wikipedia, the Free Encyclopedia.” https://en.wikipedia.org/wiki/Lucas_critique.

Mcgrayne, S. 2012. The Theory That Would Not Die: How Bayes’ Rule Cracked the Enigma Code, Hunted down Russian Submarines, and Emerged Triumphant from Two Centuries of Controversy.

Pearl, J. 2009. Causality: Models, Reasoning and Inference. 2nd ed. USA: Cambridge University Press.

Sampedro, J. L. 1983. “El Reloj, El Gato Y Madagascar.” Revista de Estudios Andaluces. https://doi.org/10.12795/rea.1983.i01.09.

Silver, N. 2012. The Signal and the Noise.

Tetlock, Philip E., and Dan Gardner. 2015. Superforecasting: The Art and Science of Prediction. Crown Publishing Group.

---

2. Esto no es rigurosamente cierto: véase la bibliografía razonada del capítulo para más información.↩︎