Comparaciones de tres grupos: pruebas vs modelos
Una pregunta reciente en r-help-es se refería a la comparación en R de las proporciones en tres grupos. Obviando algunas pequeñas complicaciones en el problema, la respuesta canónica podría ser esta:
total <- c(56, 49,51)
positivos <- c(14, 10, 17)
prop.test(tmp$positivos, tmp$positivos + tmp$negativos)
# 3-sample test for equality of proportions without continuity correction
#
# data: tmp$positivos out of tmp$positivos + tmp$negativos
# X-squared = 2.2289, df = 2, p-value = 0.3281
# alternative hypothesis: two.sided
# sample estimates:
# prop 1 prop 2 prop 3
# 0.2500000 0.2040816 0.3333333Los grupos no parecen ser desiguales.
Tengo la sospecha de que gran parte de lo que se enseña como pruebas estadísticas podría subsumirse en el estudio de modelos. Por ejemplo, así:
tmp <- data.frame(positivos = positivos,
negativos = total - positivos,
grupos = grupos)
mod.1 <- glm(cbind(positivos, negativos) ~ grupos,
data = tmp, family = binomial)
mod.0 <- glm(cbind(positivos, negativos) ~ 1,
data = tmp, family = binomial)
anova(mod.0, mod.1, test = "Chisq")
# Analysis of Deviance Table
#
# Model 1: cbind(positivos, negativos) ~ 1
# Model 2: cbind(positivos, negativos) ~ grupos
# Resid. Df Resid. Dev Df Deviance Pr(>Chi)
# 1 2 2.2129
# 2 0 0.0000 2 2.2129 0.3307La comparación de los dos modelos nos indica que la variable grupos no parece ser significativa con un p-valor similar al de más arriba.
Además,
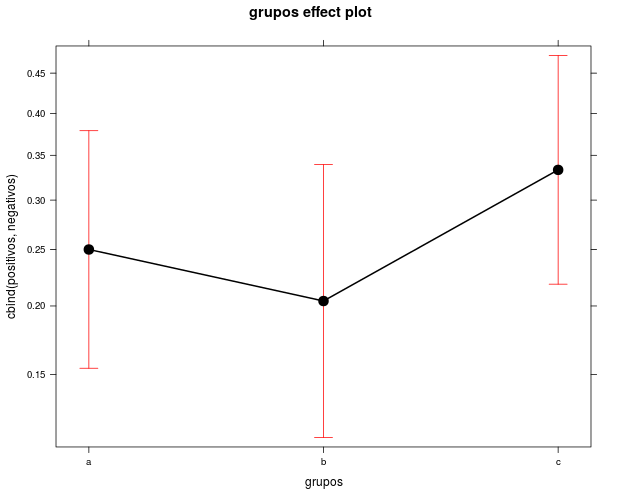
library(effects)
effects <- Effect("grupos", mod.1)
plot(effects)produce un gráfico con sus intervalos de confianza, etc.
La vía de usar modelos permite, además, considerar otras variables adicionales de control que no hay manera de contemplar con pruebas como prop.test.
En resumen, usar y comparar modelos en lugar realizar de pruebas tradicionales:
- No es ni conceptual ni implementacionalmente más complicado.
- Es más flexible y se adapta mejor a generalizaciones (como la existencia de variables explicativas adicionales).
¿Merecería la pena reevaluar y achicar el espacio que el currículo tradicional de la estadística dedica a las pruebas canónicas?