muestra_uniforme <- runif(10)
muestra_normal <- rnorm(13)12 Probabilidad, estadística y ciencia de datos con R
Esta última sección es una mínima introducción a la probabilidad y la estadística usando R. Comienza discutiendo las distribuciones de probabilidad y la generación de números aleatorios para después mostrar algunos de los algoritmos que dispone R para resolver problemas estadísticos o de la llamada ciencia de datos. Se limitará a ilustrar el uso de estas técnicas con R sin profundizar en su sustancia.
12.1 Distribuciones de probabilidad
Es frecuente querer crear vectores que sigan una determinada distribución de probabilidad. Por ejemplo, pueden obtenerse vectores con una distribución uniforme (en [0, 1]) o normal (estándar):
Ejercicio 12.1 Casi todas las distribuciones admiten parámetros adicionales. Por ejemplo, la media y la desviación estándar para la distribución normal. Consulta la ayuda de rnorm para ver cómo muestrear una variable aleatoria normal con media 1 y desviación estándar 3. Extrae una muestra de 10000 elementos de ella y comprueba que lo has hecho correctamente usando las funciones mean y sd.
Para entender la forma de esas distribuciones, podemos construir el histograma de una muestra, como a continuación:
hist(rnorm(1000))
hist(runif(1000))
hist(rpois(1000, 5))Ejercicio 12.2 Busca cómo muestrear la distribución gamma.
Ejercicio 12.3 Consulta la ayuda de rnorm, runif y rpois. ¿Qué tienen en común?
El ejercicio anterior debería poner de manifiesto cómo en R, asociada a cada distribución de probabilidad hay cuatro funciones cuyos nombres comienzan por las letras r, p, d y q. La función que comienza por r sirve para muestrear la distribución, como en los ejemplos anteriores.
La función que comienza por d es la densidad1 de la distribución. Por ejemplo, la función dnorm es la famosa campana de Gauss. Se puede representar con la función curve:
curve(dnorm(x, 0, 2), -8, 8)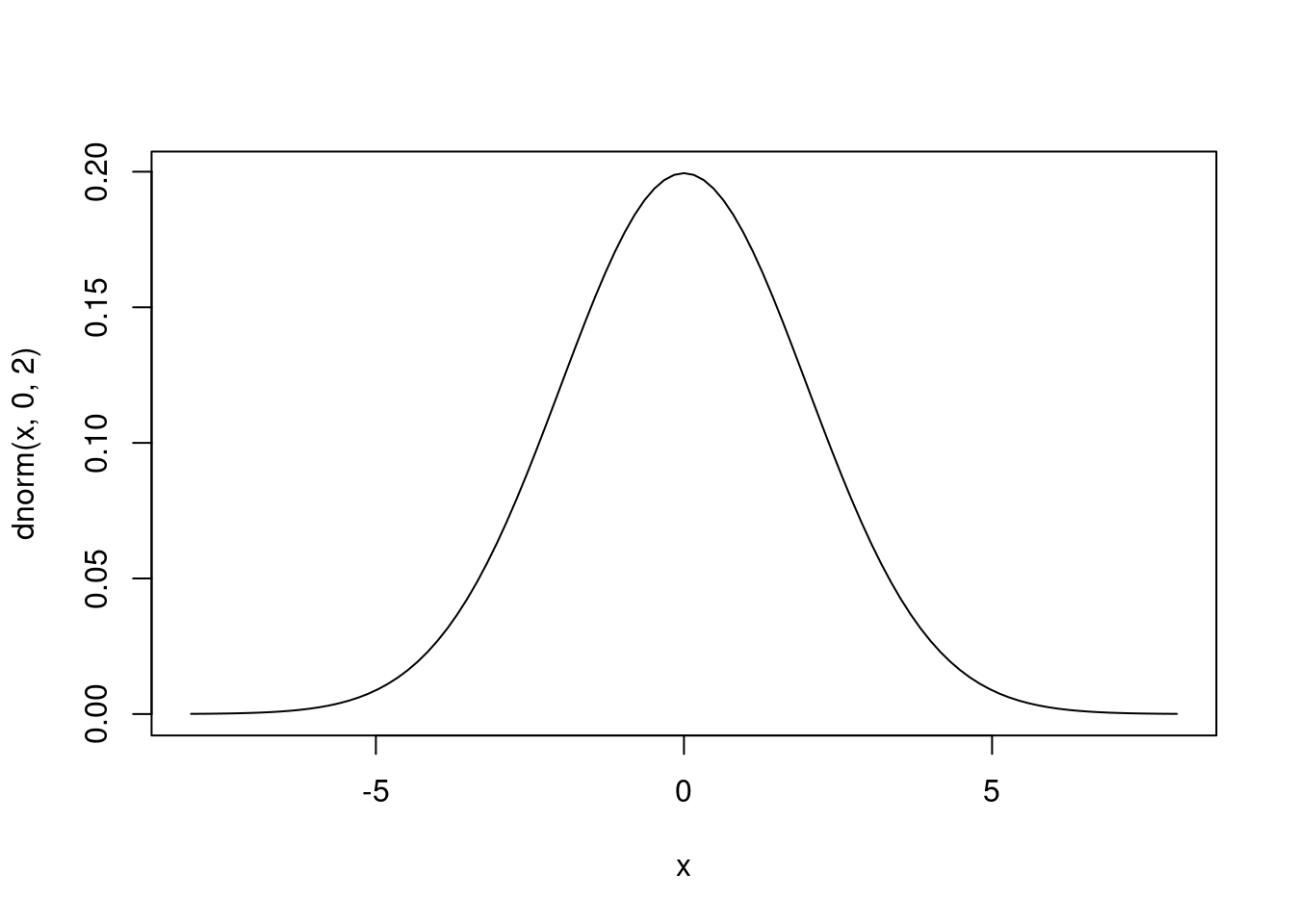
La función de densidad tiene la forma ideal a la que convergen los histogramas de las muestras de la distribución. Estos histogramas serán más parecidos a ella conforme mayor sea el tamaño de la muestra. Usando términos matemáticos, aunque con cierto abuso del lenguaje, la función de densidad es el límite de los histogramas.
Ejercicio 12.4 Usa curve para representar la densidad de la distribución beta para diversos valores de sus parámetros. Lee ?curve para averiguar cómo sobreimpresionar curvas y representa la densidad para diversas combinaciones de los parámetros con colores distintos. Puedes comparar el resultado con los gráficos que aparecen en la página de la distribución beta en la Wikipedia.
Ejercicio 12.5 Toma una distribución cualquiera y representa el histograma. Usa el ejercicio anterior para sobreimpresionar la función de densidad sobre el histograma. Nota: recuerda que el histograma puede representar frecuencias o proporciones; usa las segundas.
La función que comienza por p es la función de probabilidad, que es la integral de la densidad. En concreto, si la función de densidad es \(f\), la función de probabilidad, \(F\), es
\[ F(x) = \int_{-\infty}^x f(x) dx. \]
Como consecuencia, es una función que crece más o menos suavemente de 0 a 1.
curve(pnorm(x, 0, 2), -8, 8)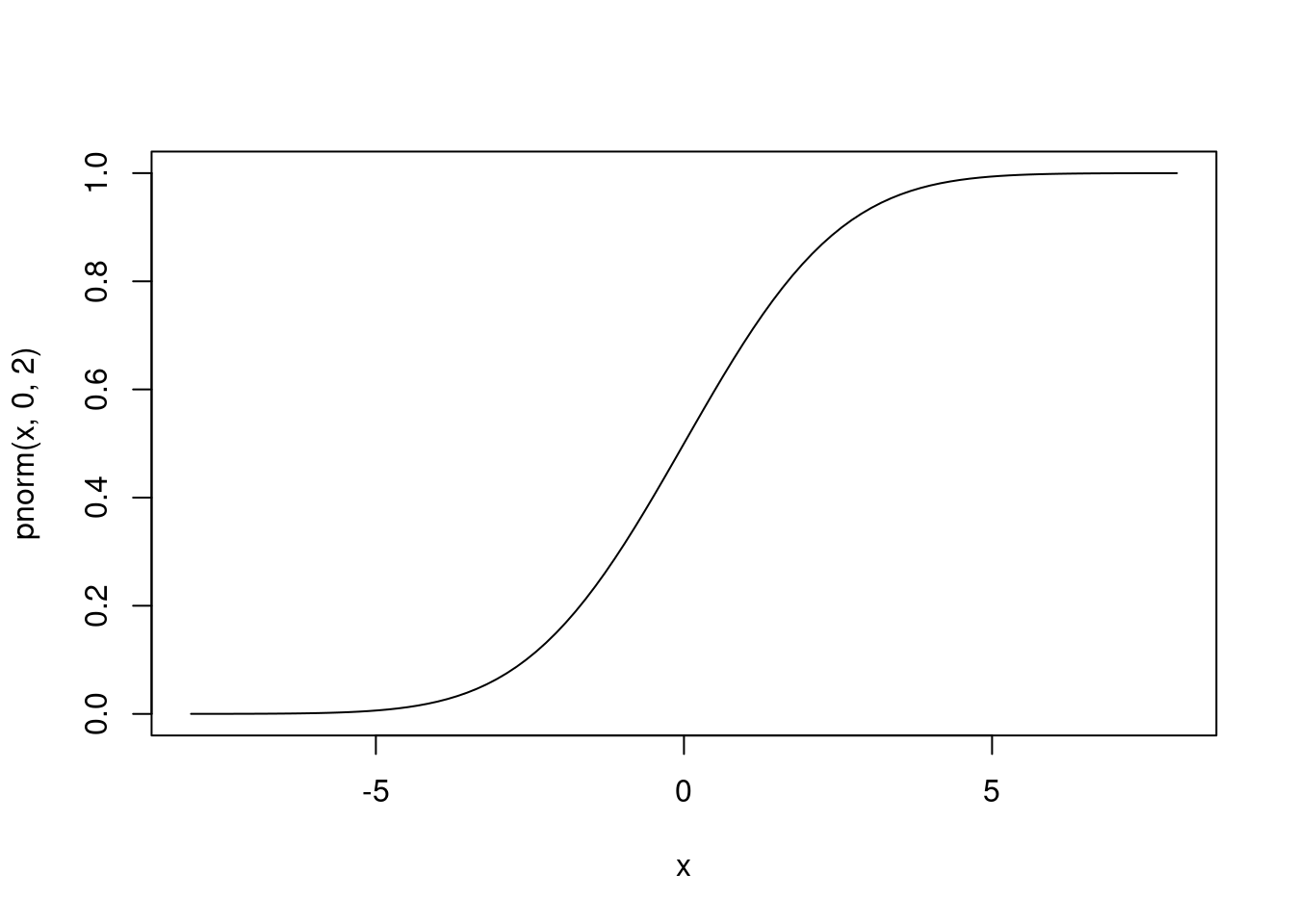
Si \(X\) es una variable aleatoria con una función de probabilidad \(F\), entonces \(F(x) = P(X < x)\). Los eventos \(X < x\) son tan importantes que sus probabilidades se precalculan en \(F\).
Finalmente, la función cuyo nombre comienza por q es la que calcula los cuantiles. Es decir, es la inversa de la función de probabilidad. Por ejemplo, en el gráfico
curve(dnorm(x, 0, 2), -8, 8)
abline(v = qnorm(0.1, 0, 2), col = "red")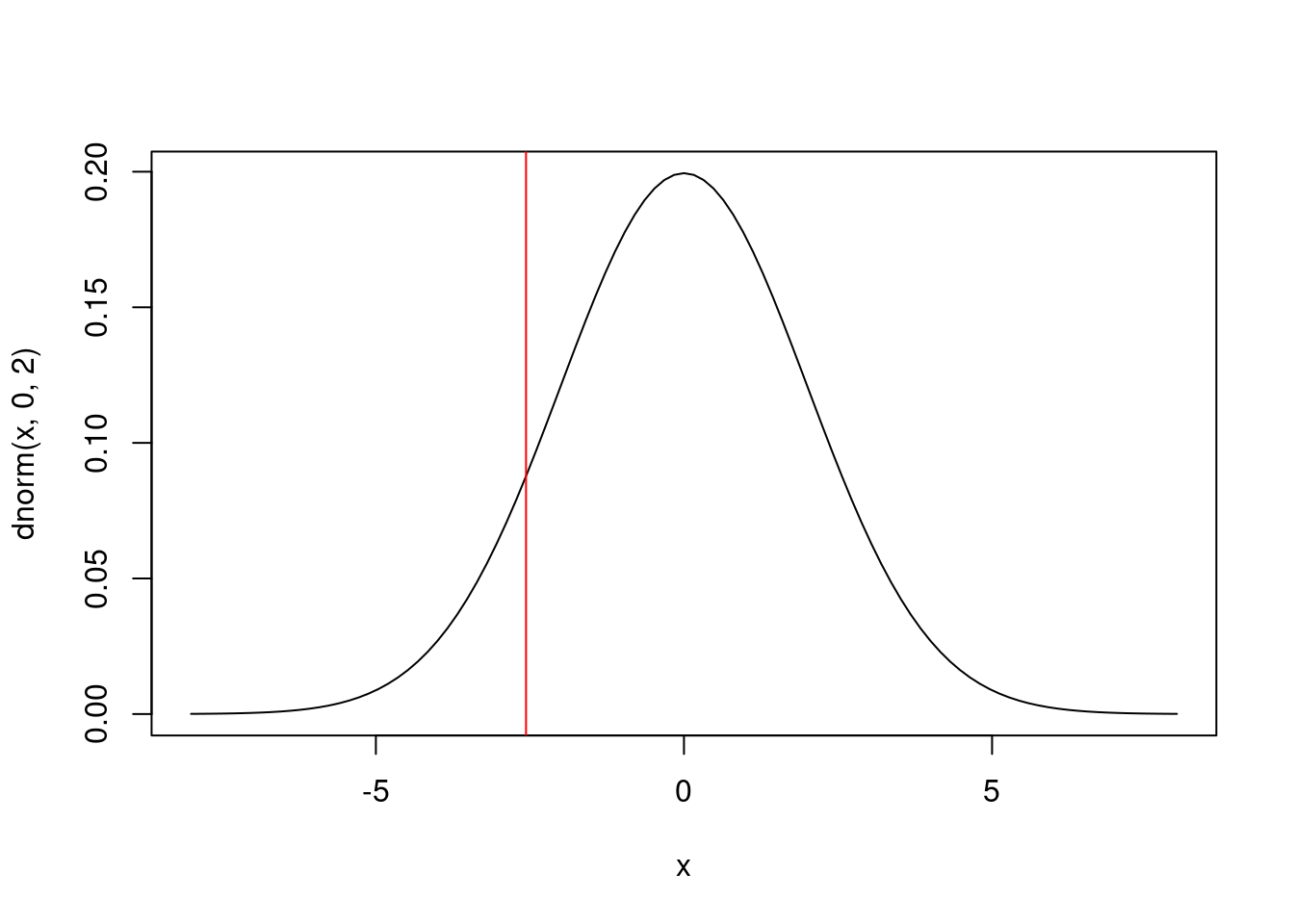
la probabilidad que asigna la normal a la zona que queda a la izquierda de la recta vertical roja es del 10%, valor indicado por el primer argumento de qnorm, 0.1.
12.2 Árboles de decisión
Los árboles de decisión son útiles para entender la estructura de un conjunto de datos. Sirven para resolver problemas tanto de clasificación (predecir una variable discreta, típicamente binaria) como de regresión (predecir una variable continua). Se trata de modelos excesivamente simples pero, y ahí reside fundamentalmente su interés, fácilmente interpretables.
Existen varios paquetes en R para construir árboles de decisión. De entre todos ellos, vamos a usar los de la librería party:
library(party)Vamos a analizar los datos de Olive.txt, que describen una muestra de diversos aceites de oliva italianos. Para cada aceite se ha anotado su procedencia (Region y Area) y una serie de caracterísicas químicas, las concentraciones de determinados ácidos (como el eicosenoico). Este conjunto de datos se compiló para poder crear un modelo que distinguiese la procedencia del aceite a través de pruebas químicas y evitar así fraudes de reetiquetado. Nuestro objetivo será, por tanto, predecir la zona de procedencia a partir de la huella química de los aceites, es decir, usando esas concentraciones químicas como potenciales predictores del origen de los distintos aceites.
En primer lugar vamos a leer y preparar los datos. Vamos a tratar de predecir la Region, por lo que eliminaremos las variables Area y la auxiliar Test.Training.
olive <- read.table("data/Olive.txt", header = T, sep = "\t")
olive_00 <- olive
olive_00$Area <- olive_00$Test.Training <- NULL
olive_00$Region <- factor(olive_00$Region)A continuación, crearemos el modelo.
modelo <- ctree(Region ~ ., data = olive_00)La fórmula Region ~ . indica que queremos modelar Region en función de ., es decir, el resto de las variables disponibles en nuestros datos. Alternativamente, se pueden indicar las variables predictoras a la derecha de ~ separadas por el signo +: y ~ x1 + x2 + x3. También es posible seleccionar todas menos algunas de ellas con el signo -, p.e., y ~ . - x1. Desafortunadamente, la función ctree no interpreta correctamente expresiones que usan el signo -. Ese es el motivo por el que hemos creado un conjunto de datos auxiliar olive_00; lo natural hubiese sido especificar Region ~ . - Area - Test.Training.
El objeto modelo construido con ctree contiene toda la información relativa al árbol que hemos construido. La mejor manera de inspeccionar el modelo obtenido es representándolo gráficamente haciendo:
plot(modelo)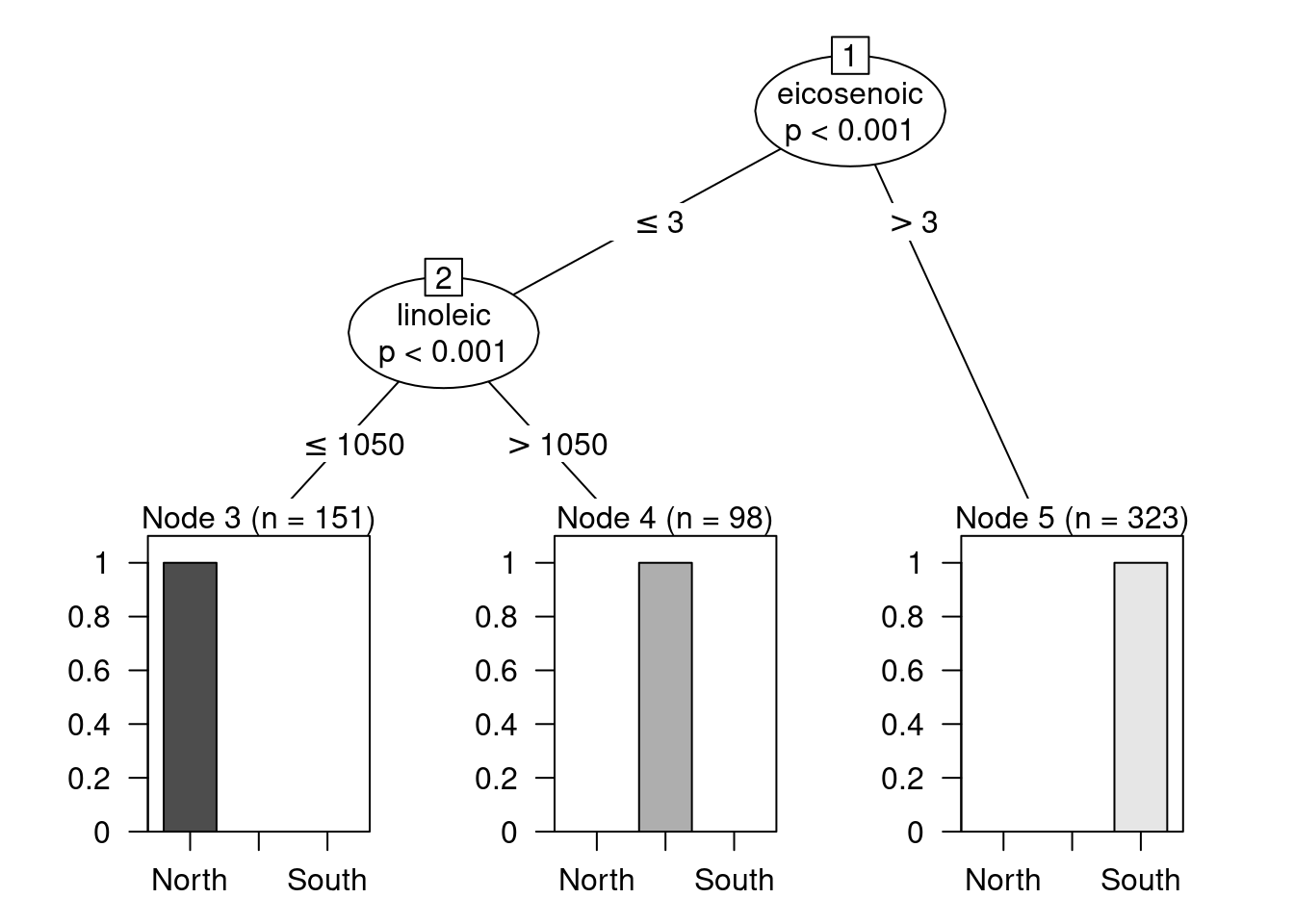
Como puede apreciarse, la predicción es perfecta: en los nodos finales no hay confusión de regiones. Por ejemplo, el nodo terminal de la derecha, el que se construye con la regla eicosenoic > 3, contiene únicamente aceites procedentes de la zona sur de Italia. Por lo tanto, siempre que un aceite cumpla dicha regla, se categorizará como procedente de esa región.
Si en el gráfico resultante no puedes apreciar correctamente los nodos terminales o sus etiquetas, trata de ampliar la ventana gráfica. Si aun ampliándola siguiesen sin verse adecuadamente, guarda el gráfico con una resolución alta en disco y ábrelo con un programa de visualización de imágenes.
Ejercicio 12.6 Describe las reglas que definen los otros dos nodos terminales y las decisiones que se tomarán con los aceites que caigan en ellos.
Normalmente, para medir el poder predictivo de un modelo, se utiliza un conjunto de datos para entrenar el modelo y otro distinto para evaluarlo. Nuestro conjunto de datos sugiere realizar la partición de acuerdo con la columna (que suponemos generada al azar) Test.Training. Para ello usaremos la función split:
olive_01 <- olive
olive_01$Area <- NULL
olive_01$Region <- factor(olive_01$Region)
olive_01 <- split(olive_01, olive_01$Test.Training)En el código anterior hemos partido el conjunto de datos en dos trozos en función de la columna Test.Training.
Ejercicio 12.7 Inspecciona el objeto olive_01.
Ahora usaremos la parte Training para ajustar el modelo:
olive_01$Training$Test.Training <- NULL
modelo <- ctree(Region ~ ., data = olive_01$Training)
plot(modelo)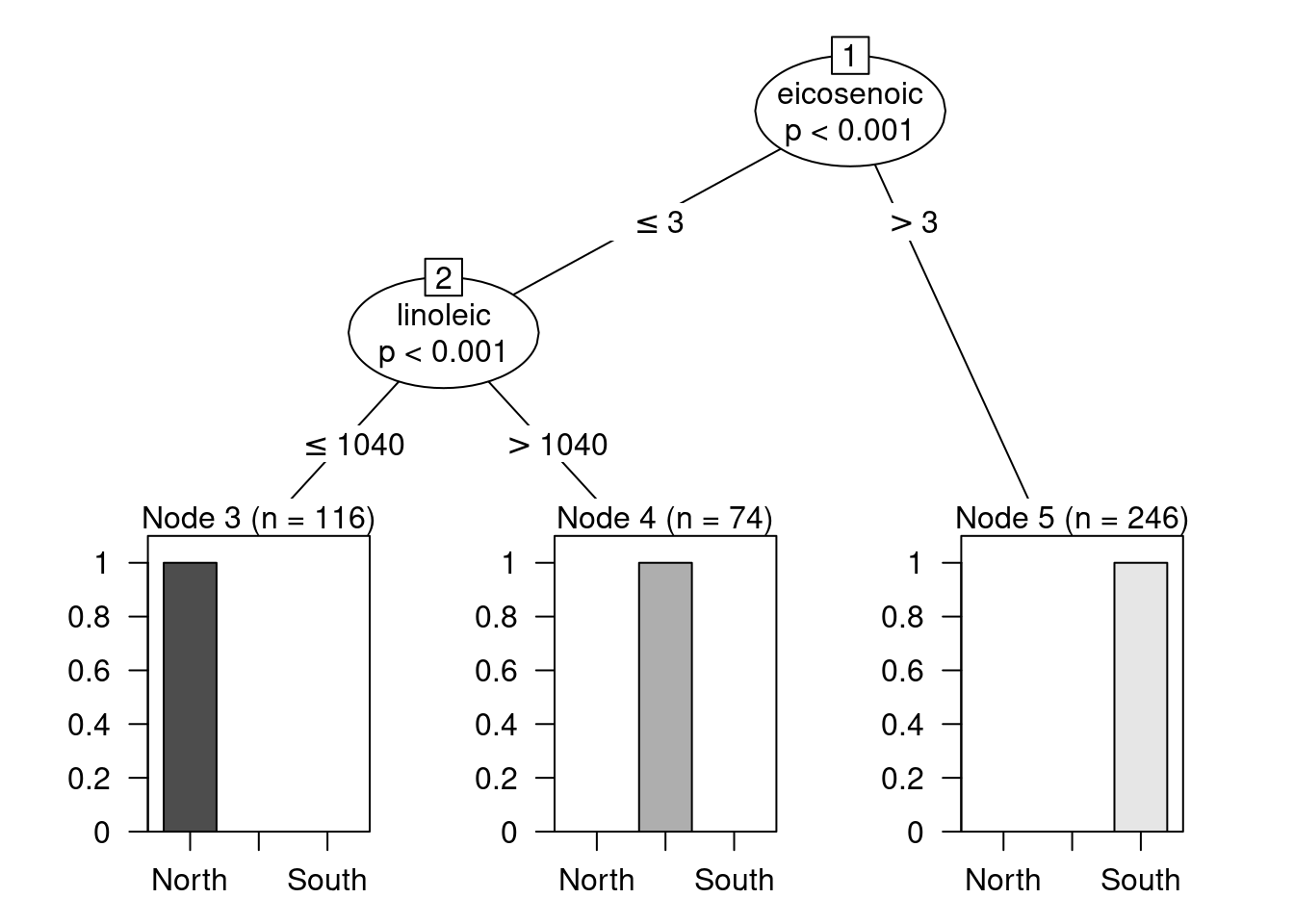
El modelo resultante es muy similar construido con todos los datos. Pero ahora podemos hacer predicciones usando la parte Test2 con la función predict.
predicciones <- predict(modelo, olive_01$Test)La práctica totalidad de los modelos estadíticos en R implementan una versión de predict que siempre admite dos argumentos3: el modelo ajustado previamente y un nuevo conjunto de datos (obviamente, con la misma estructura que el usado para crearlo).
Una vez obtenidas las predicciones, se pueden comparar con los valores originales. La expresión
mean(predicciones == olive_01$Test$Region)[1] 0.9926471calcula la proporción de aciertos.
Ejercicio 12.8 ¿Por qué?
Ejercicio 12.9 Cuenta los aciertos y los fallos.
Para ver dónde se han cometido los errores, se puede hacer
table(predicciones, olive_01$Test$Region)
predicciones North Sardinia South
North 34 0 0
Sardinia 1 24 0
South 0 0 77que construye una tabla que, idealmente, debería tener una estructura diagonal. Eso correspondería al caso en que cada aceite se asigna a la región a la que realmente pertenece. Sin embargo, el modelo comete un (único) error al asignar a Cerdeña un aceite que, en realidad, es de la región norte.
Ejercicio 12.10 Repite el ejercicio anterior (predicción) usando la variable Area en lugar de Region. En este caso el modelo no es tan bueno porque hay más áreas que regiones y algunas están tan próximas entre sí que es natural que las diferencias entre sus aceites no sean tan acusadas como entre regiones.
Ejercicio 12.11 Los bosques aleatorios son más potentes que los árboles que hemos visto arriba. Busca en internet cuál es el paquete y la función que sirve para crear un modelo de bosques aleatorios y repite el ejercicio anterior con él. ¿Funcionan mejor?
El ejercicio anterior sirve de ilustración de cómo en R muchos modelos tienen una interfaz similar. Solo en algunos casos particulares es necesario utilizar sintaxis especiales.
12.3 Igualdad de medias y t-test
Los datos que vamos a usar están bajados de http://archive.ics.uci.edu/ml/datasets/Student+Performance. Se refieren al desempeño académico de una serie de alumnos portugueses en función de una serie de indicadores sociodemográficos.
mat.por <- read.table("data/student-mat.csv", header = T, sep = ";")Las variables G1, G2 y G3 se refieren a las notas obtenidas en tres exámenes distintos y nuestro objetivo será analizar las diferencias por sexos en el último examen, G3. Primero, gráficamente, con un diagrama de cajas:
boxplot(mat.por$G3 ~ mat.por$sex, col = "gray", xlab = "sexo", ylab = "nota final")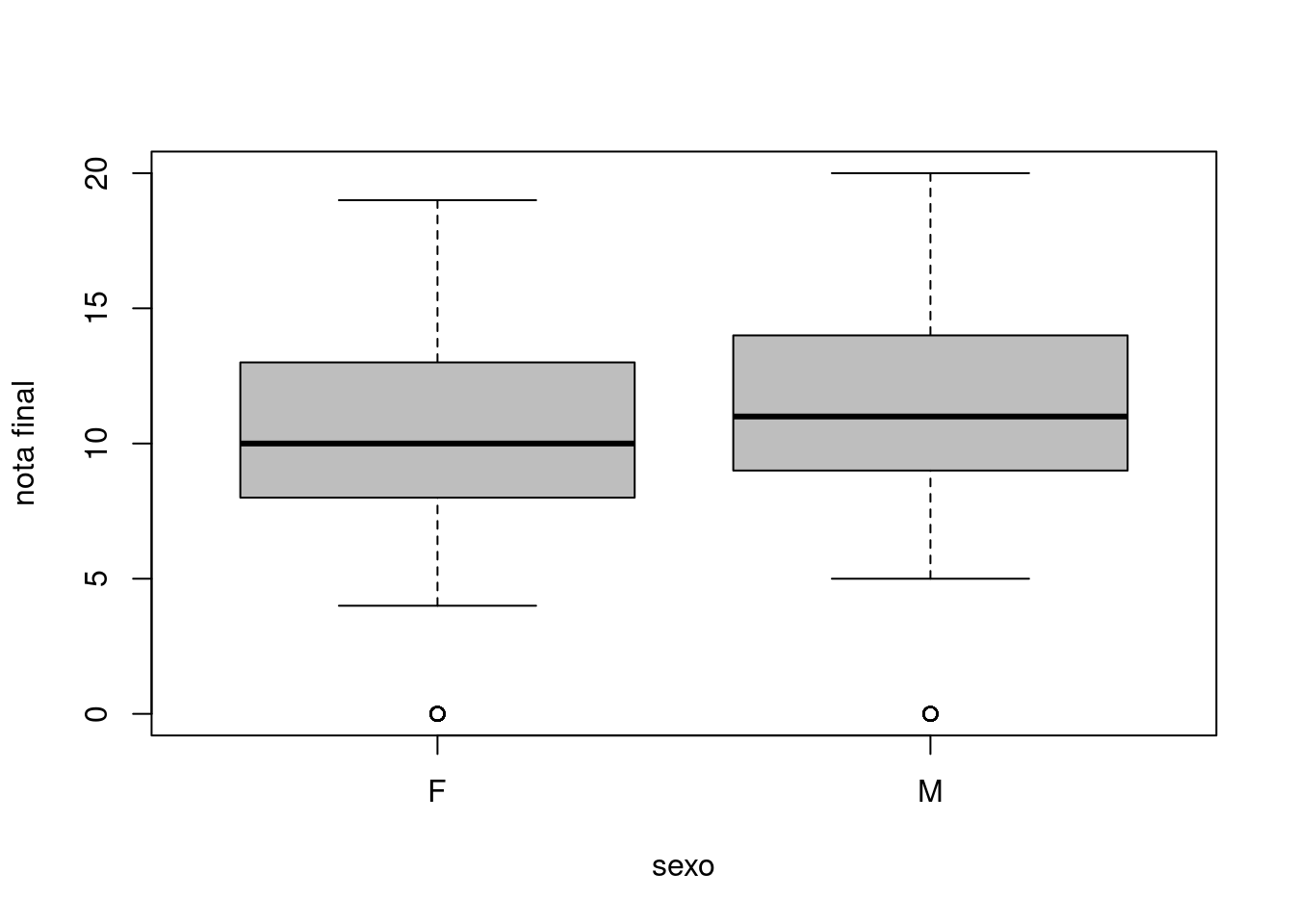
Se aprecia una pequeña diferencia en favor de los chicos. Es la diferencia observada, que puede deberse al azar. Por eso se puede aplicar una prueba estadística (en este caso, el llamado test de Student o t-test) para determinar si esa diferencia observada es o no significativa:
res <- t.test(mat.por$G3 ~ mat.por$sex)
res
Welch Two Sample t-test
data: mat.por$G3 by mat.por$sex
t = -2.0651, df = 390.57, p-value = 0.03958
alternative hypothesis: true difference in means between group F and group M is not equal to 0
95 percent confidence interval:
-1.85073226 -0.04545244
sample estimates:
mean in group F mean in group M
9.966346 10.914439 El objeto res contiene la información relevante sobre la prueba realizada y al ser imprimido muestra un resumen, el típico resumen que suele mostrarse en los estudios en el que se aplica: el intervalo de confianza para la diferencia de medias de interés y el p-valor correspondiente. En este caso el p-valor es ligeramente inferior al umbral habitual de 0.05, por lo que en muchos contextos se hablaría de rechazar la hipótesis de igualdad de medias efectivamente aceptando un peor desempeño académico de las chicas en este examen con respecto a sus homólogos masculinos.
El p-valor, por si interesase utilizarlo para otros fines, puede extraerse así:
res$p.value[1] 0.039577Ejercicio 12.12 res es un objeto, ¿de qué clase? También es una lista: examínala. ¿Puedes identificar en ella todos los elementos que forman parte del resumen mostrado más arriba?
Ejercicio 12.13 Busca en Google r non parametric alternative to t-test e identifica un test no paramétrico alternativo al t-test. Úsalo para determinar si las notas finales entre sexos “son o no iguales”.
Pruebas estadíticas similares a las anteriores se realizan habitualmente para, por ejemplo, comparar el desempeño (en términos, p.e., de conversiones) entre dos versiones de una página web, de dos campañas publicitarias distintas, de dos tratamientos médicos alternativos, etc.
12.4 Igualdad de medias mediante remuestreos
No es necesario utilizar pruebas estadísticas de libro para resolver el problema de la igualdad de medias (entre otros). Es más instructivo (e incluso tiene un alcance más largo) usar los ordenadores para crear pruebas ad hoc mediante remuestreos. La idea subyacente es la siguiente:
- El desempeño de dos grupos elegidos al azar nunca va a ser idéntico: tiene una variabilidad natural.
- Creando grupos al azar y midiendo la diferencia de desempeño puede medirse esa variabilidad natural.
- Cuando la diferencia entre dos grupos definidos por una determinada variable exceda esa variabilidad natural, podrá decirse que los grupos son distintos. Si no, no habría motivos para ello.
Podemos implementar esa estrategia en R. Para ello, primero, debemos calcular la diferencia entre chicos y chicas:
g3 <- mat.por$G3
sex <- mat.por$sex
medias.sexo <- tapply(g3, sex, mean)
diferencia.original <- medias.sexo["M"] - medias.sexo["F"]diferencia.original es la diferencia de medias observada en los datos. En el código que sigue vamos a asignar a los alumnos etiquetas al azar y medir las diferencias entre los grupos definidos por ellas. Lo haremos varias veces y luego veremos si la diferencia original es normal o si se sale de rango.
Para ello, primero, construiremos la función de remuestreo. Esta función aleatoriza el sexo. Eso quiere decir que asigna a los individuos una etiqueta M o F aleatoria y mide las diferencias obtenidas entre ambos grupos. Como las etiquetas se distribuyen al azar, no se esperarían diferencias de comportamiento entre los grupos. Obviamente, los promedios nunca van a ser exactamente iguales y esas diferencias (que son puro ruido estadístico) nos ayudan a determinar mediante su comparación en qué medida la diferencia entre los grupos definidos por el sexo encierran un efecto real.
remuestrea <- function(){
tmp <- tapply(g3, sample(sex), mean)
tmp["M"] - tmp["F"]
}Luego podemos llamar a esa función muchas veces para obtener otras tantas simulaciones:
diferencias.simuladas <- replicate(10000, remuestrea())En este momento disponemos de una muestra de 10000 diferencias entre grupos sin señal. De otra manera, hemos identificado el nivel de ruido del conjunto de datos, que podemos representar con un histograma. Sobre él podemos representar la diferencia real (con una línea vertical roja):
hist(diferencias.simuladas)
abline(v = diferencia.original, col = "red")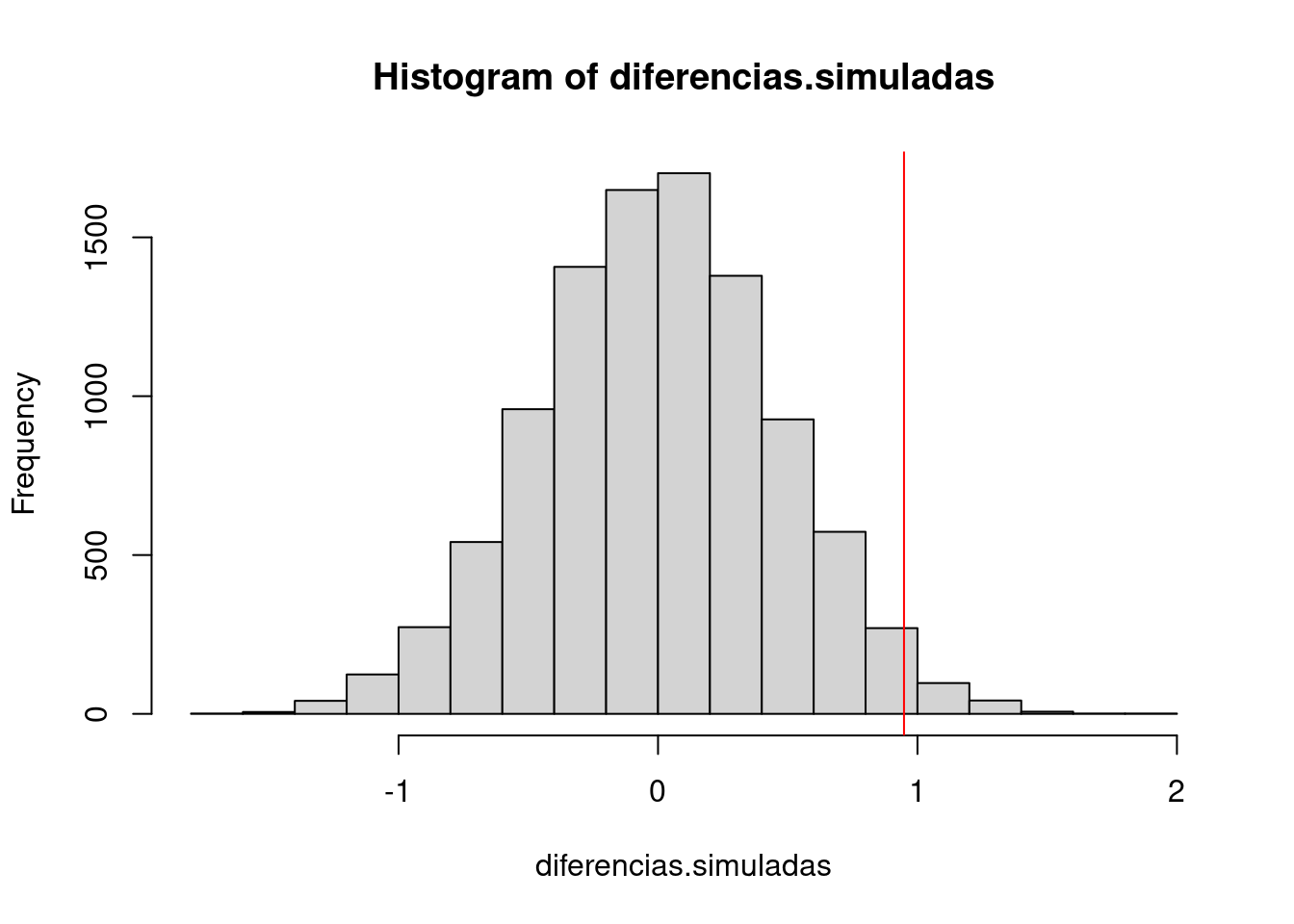
La gráfica obtenida representa la diferencia original (por sexos) dentro del universo de diferencias sin señal creadas mediante remuestreos. El p-valor (que hemos obtenido antes mediante una prueba estadística clásica) no es otra cosa que la proporción de observaciones que caen a la derecha de la línea roja. Lo podemos calcular explícitamente así:
mean(diferencias.simuladas > diferencia.original)[1] 0.0197Como se ve, aunque no exactamente igual, es similar al calculado más arriba.
En realidad, está más próxima a la mitad del p-valor calculado arriba. Esto se debe a que antes se ha calculado el p-valor correspondiente a la prueba de que la diferencia de medias sea igual a cero. En las simulaciones hemos calculado el de que esta diferenicia sea menor que cero. En un caso se trata de una de las llamadas pruebas bilaterales y en el otro, de las unilaterales. No vamos a adentrarnos en las diferencias entre ambas.
12.5 Regresión lineal
La regresión lineal (al menos en el caso más simple de una sola variable predictora) identifica la recta óptima que atraviesa una nube de puntos. En el caso que se muestra a continuación, la construida representando gráficamente la nota de los alumnos en los exámenes segundo y tercero, i.e., G2 y G3:
plot(mat.por$G2, mat.por$G3,
main = "Notas en el segundo y tercer examen",
xlab = "Segundo examen", ylab = "Tercer examen")
modelo.00 <- lm(G3 ~ G2, data = mat.por)
abline(modelo.00, col = "red")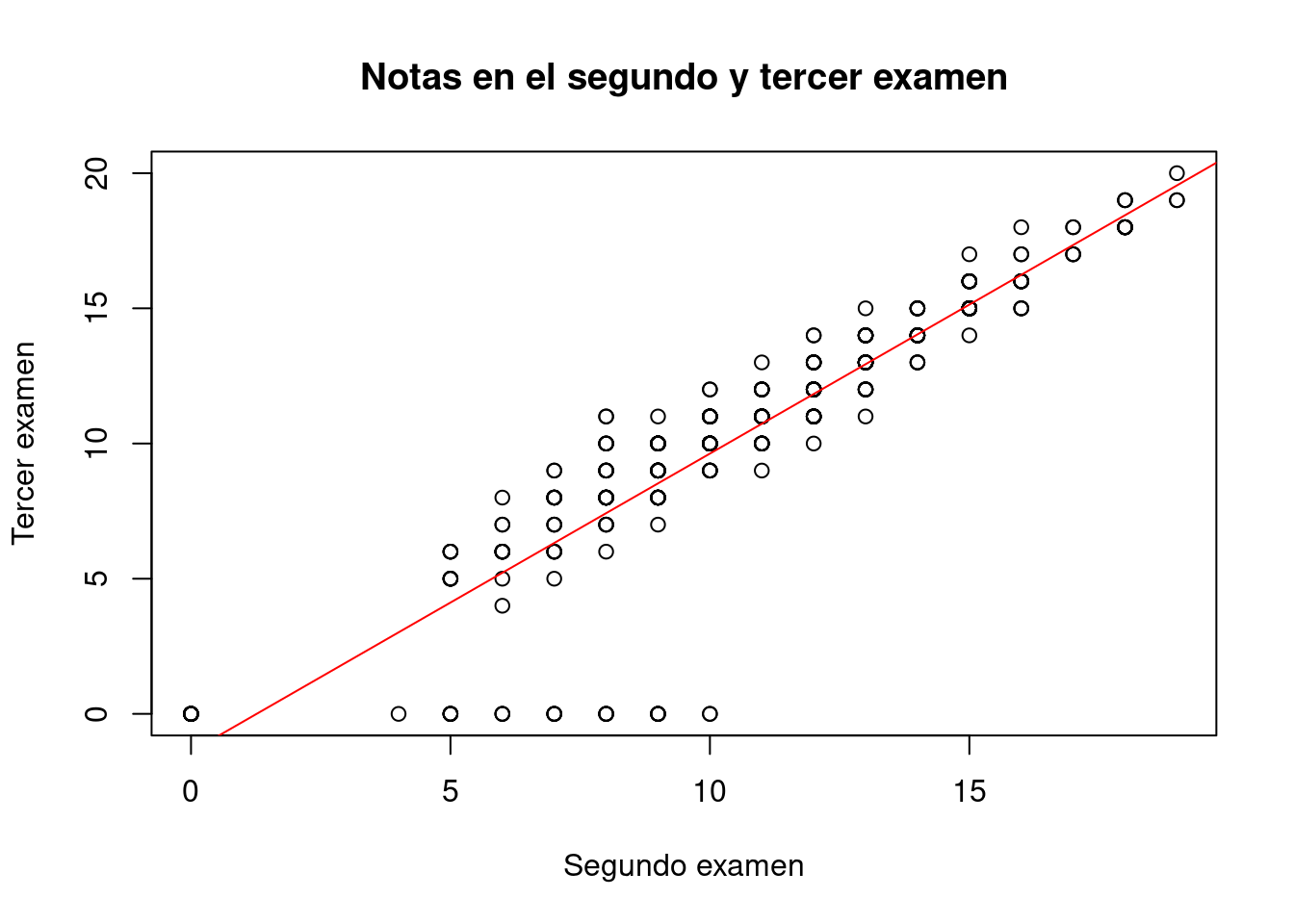
En el código anterior hemos representado nuestros datos con una gráfica de dispersión y hemos creado un modelo lineal para encontrar la recta que mejor se ajusta a los datos. Luego la hemos representado con la función abline en rojo. Advierte cómo abline es capaz de interpretar los coeficientes del modelo para representar la recta: no es necesario indicárselos explícitamente.
En las publicaciones científicas se suele resumir un modelo lineal mediante una tabla y algunos indicadores adicionales (como la \(R^2\)). La función summary proporciona dicha información:
summary(modelo.00)
Call:
lm(formula = G3 ~ G2, data = mat.por)
Residuals:
Min 1Q Median 3Q Max
-9.6284 -0.3326 0.2695 1.0653 3.5759
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -1.39276 0.29694 -4.69 3.77e-06 ***
G2 1.10211 0.02615 42.14 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.953 on 393 degrees of freedom
Multiple R-squared: 0.8188, Adjusted R-squared: 0.8183
F-statistic: 1776 on 1 and 393 DF, p-value: < 2.2e-16Cabría esperar que la nota del segundo examen fuese muy similar a la del primero. Es decir, que la recta de regresión fuese aproximadamente y = x; dicho de otra manera, que los coeficientes del modelo fuesen 0 y 1. Sin embargo, no ocurre así: por cada punto en el primer examen, los alumnos sacan 1.1 puntos en el segundo; pero comienzan con un hándicap de -1.39 puntos. Eso es extraño y por eso se plantea el siguiente ejercicio.
Ejercicio 12.14 Las observaciones con valor G3 == 0, fácilmente identificables en el gráfico de dispersión mostrado más arriba, parecen estar sesgando el modelo. Elimínalas y repite el análisis anterior.
El ejercicio anterior pone de manifiesto lo fundamental de un análisis visual de los datos previo a su modelización estadística. No obstante, los diagnósticos de la regresión, es decir, el estudio de sus resultados, también permite identificar a posteriori este tipo de problemas.
Ejercicio 12.15 Estas observaciones pudieran haber afectado tambiél al t-test anterior. Repítelo después de eliminar esas observaciones.
La regresión lineal puede utilizarse con más de una única variable predictora, como a continuación:
modelo.10 <- lm(G3 ~ ., data = mat.por)
summary(modelo.10)
Call:
lm(formula = G3 ~ ., data = mat.por)
Residuals:
Min 1Q Median 3Q Max
-7.9339 -0.5532 0.2680 0.9689 4.6461
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -1.115488 2.116958 -0.527 0.598573
schoolMS 0.480742 0.366512 1.312 0.190485
sexM 0.174396 0.233588 0.747 0.455805
age -0.173302 0.100780 -1.720 0.086380 .
addressU 0.104455 0.270791 0.386 0.699922
famsizeLE3 0.036512 0.226680 0.161 0.872128
PstatusT -0.127673 0.335626 -0.380 0.703875
Medu 0.129685 0.149999 0.865 0.387859
Fedu -0.133940 0.128768 -1.040 0.298974
Mjobhealth -0.146426 0.518491 -0.282 0.777796
Mjobother 0.074088 0.332044 0.223 0.823565
Mjobservices 0.046956 0.369587 0.127 0.898973
Mjobteacher -0.026276 0.481632 -0.055 0.956522
Fjobhealth 0.330948 0.666601 0.496 0.619871
Fjobother -0.083582 0.476796 -0.175 0.860945
Fjobservices -0.322142 0.493265 -0.653 0.514130
Fjobteacher -0.112364 0.601448 -0.187 0.851907
reasonhome -0.209183 0.256392 -0.816 0.415123
reasonother 0.307554 0.380214 0.809 0.419120
reasonreputation 0.129106 0.267254 0.483 0.629335
guardianmother 0.195741 0.252672 0.775 0.439046
guardianother 0.006565 0.463650 0.014 0.988710
traveltime 0.096994 0.157800 0.615 0.539170
studytime -0.104754 0.134814 -0.777 0.437667
failures -0.160539 0.161006 -0.997 0.319399
schoolsupyes 0.456448 0.319538 1.428 0.154043
famsupyes 0.176870 0.224204 0.789 0.430710
paidyes 0.075764 0.222100 0.341 0.733211
activitiesyes -0.346047 0.205938 -1.680 0.093774 .
nurseryyes -0.222716 0.254184 -0.876 0.381518
higheryes 0.225921 0.500398 0.451 0.651919
internetyes -0.144462 0.287528 -0.502 0.615679
romanticyes -0.272008 0.219732 -1.238 0.216572
famrel 0.356876 0.114124 3.127 0.001912 **
freetime 0.047002 0.110209 0.426 0.670021
goout 0.012007 0.105230 0.114 0.909224
Dalc -0.185019 0.153124 -1.208 0.227741
Walc 0.176772 0.114943 1.538 0.124966
health 0.062995 0.074800 0.842 0.400259
absences 0.045879 0.013412 3.421 0.000698 ***
G1 0.188847 0.062373 3.028 0.002645 **
G2 0.957330 0.053460 17.907 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.901 on 353 degrees of freedom
Multiple R-squared: 0.8458, Adjusted R-squared: 0.8279
F-statistic: 47.21 on 41 and 353 DF, p-value: < 2.2e-16En este modelo hemos incluido todas las variables predictoras. La tabla obtenida muestra cómo dos de la más importantes para predecir la nota final son G1 y G2. Lo cual tiene mucho sentido. Pero, a la vez, bajo cierto punto de vista, es poco instructivo. Nos gustaría más saber cómo afectan las variables sociodemográficas a la nota obtenida en un examen (y no constatar que quienes sacan buenas notas tienden a seguir sacándolas). Por eso podemos repetir el ejercicio eliminando dichas variables.
modelo.11 <- lm(G3 ~ . - G1 - G2, data = mat.por)
summary(modelo.11)
Call:
lm(formula = G3 ~ . - G1 - G2, data = mat.por)
Residuals:
Min 1Q Median 3Q Max
-13.0442 -1.9028 0.4289 2.7570 8.8874
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 14.07769 4.48089 3.142 0.00182 **
schoolMS 0.72555 0.79157 0.917 0.35997
sexM 1.26236 0.50003 2.525 0.01202 *
age -0.37516 0.21721 -1.727 0.08501 .
addressU 0.55135 0.58412 0.944 0.34586
famsizeLE3 0.70281 0.48824 1.439 0.15090
PstatusT -0.32010 0.72390 -0.442 0.65862
Medu 0.45687 0.32317 1.414 0.15833
Fedu -0.10458 0.27762 -0.377 0.70663
Mjobhealth 0.99808 1.11819 0.893 0.37268
Mjobother -0.35900 0.71316 -0.503 0.61500
Mjobservices 0.65832 0.79784 0.825 0.40985
Mjobteacher -1.24149 1.03821 -1.196 0.23257
Fjobhealth 0.34767 1.43796 0.242 0.80909
Fjobother -0.61967 1.02304 -0.606 0.54509
Fjobservices -0.46577 1.05697 -0.441 0.65972
Fjobteacher 1.32619 1.29654 1.023 0.30707
reasonhome 0.07851 0.55380 0.142 0.88735
reasonother 0.77707 0.81757 0.950 0.34252
reasonreputation 0.61304 0.57657 1.063 0.28839
guardianmother 0.06978 0.54560 0.128 0.89830
guardianother 0.75010 0.99946 0.751 0.45345
traveltime -0.24027 0.33897 -0.709 0.47889
studytime 0.54952 0.28765 1.910 0.05690 .
failures -1.72398 0.33291 -5.179 3.75e-07 ***
schoolsupyes -1.35058 0.66693 -2.025 0.04361 *
famsupyes -0.86182 0.47869 -1.800 0.07265 .
paidyes 0.33975 0.47775 0.711 0.47746
activitiesyes -0.32953 0.44494 -0.741 0.45942
nurseryyes -0.17730 0.54931 -0.323 0.74706
higheryes 1.37045 1.07780 1.272 0.20437
internetyes 0.49813 0.61956 0.804 0.42192
romanticyes -1.09449 0.46925 -2.332 0.02024 *
famrel 0.23155 0.24593 0.942 0.34706
freetime 0.30242 0.23735 1.274 0.20345
goout -0.59367 0.22451 -2.644 0.00855 **
Dalc -0.27223 0.33087 -0.823 0.41120
Walc 0.26339 0.24801 1.062 0.28896
health -0.17678 0.16101 -1.098 0.27297
absences 0.05629 0.02897 1.943 0.05277 .
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 4.108 on 355 degrees of freedom
Multiple R-squared: 0.2756, Adjusted R-squared: 0.196
F-statistic: 3.463 on 39 and 355 DF, p-value: 3.317e-10Ejercicio 12.16 Examina los \(R^2\) de ambos modelos: ¿cómo han cambiado? ¿Por qué? Nota: el indicador \(R^2\) es una medida de la bondad del ajuste, i.e., de la diferencia entre los datos y sus predicciones. Tiene el valor 1 si el ajuste es perfecto y 0 cuando el modelo no dice absolutamente nada acerca de la variable de interés.
La tabla de coeficientes mostrada más arriba se utiliza para interpretar el modelo: ver qué variables son las más importantes, en qué medida influyen en la variable de interés, etc. Sin embargo, es evidente que la interpretación es complicada cuando el número de coeficientes crece. Modelos como los presentados más arriba, los árboles, son más fáciles de interpretar. De ahí el siguiente ejercicio.
Ejercicio 12.17 Usa árboles para tratar de entender mejor el conjunto de datos y las variables que afectan a las notas finales. ¿Ves alguna variable que pueda ayudar a explicar la diferencia de desempeño entre chicos y chicas?
12.6 Regresión logística
La regresión logística se usa para predecir (y explicar) una variable binaria. A continuación estudiaremos un conjunto de datos que trata de explicar los factores que afectan a la admisión de alumnos en determinadas universidades estadounidenses como la nota en una serie de exámentes previos o la categoría de su escuela de educación secundaria.
Primero, vamos a leer los datos:
admitidos <- read.table("data/admitidos.csv", header = T, sep = "\t")
admitidos$rank <- factor(admitidos$rank)Luego, vamos a ajustar el modelo usando la función glm (para modelos lineales generalizados). La sintaxis es similar a la usada más arriba con lm; cambia, esencialmente, la familia. El modelo logístico corresponde a family = binomial; las opciones gaussian y poisson corresponden al modelo lineal habitual (para modelar variables continuas) y al de Poisson (para modelar conteos).
La función summary genera una tabla similar a la obtenida con lm.
modelo.logistico <- glm(admit ~ ., data = admitidos,
family = binomial)
summary(modelo.logistico)
Call:
glm(formula = admit ~ ., family = binomial, data = admitidos)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.6268 -0.8662 -0.6388 1.1490 2.0790
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -3.989979 1.139951 -3.500 0.000465 ***
gre 0.002264 0.001094 2.070 0.038465 *
gpa 0.804038 0.331819 2.423 0.015388 *
rank2 -0.675443 0.316490 -2.134 0.032829 *
rank3 -1.340204 0.345306 -3.881 0.000104 ***
rank4 -1.551464 0.417832 -3.713 0.000205 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 499.98 on 399 degrees of freedom
Residual deviance: 458.52 on 394 degrees of freedom
AIC: 470.52
Number of Fisher Scoring iterations: 4La variable rank es categórica. El coeficiente rank2 (negativo) muestra cómo la probabilidad de ser admitido decrece en las escuelas del segundo nivel con respecto a las del primero, que es implícito. La misma interpretación tienen los coeficientes rank3 y rank4. R elige el nivel de referencia, en este caso el 1, por estricto orden alfabético salvo que se especifique explícitamente4 lo contrario.
Ejercicio 12.18 ¿Cuántos puntos en el GRE son necesarios para compensar el haber estudiado la secundaria en una escuela de segundo nivel y no del primero?
Ejercicio 12.19 El coeficiente de la variable gre es muy pequeño con respecto al de gpa. Eso se debe a la distinta escala en la que se puntúan ambos exámenes. Una de las maneras de comparar la importancia relativa de los dos exámenes consiste en normalizar los datos. Hazlo, crea otro modelo y discute los resultados.
12.7 Modelos no lineales
En ocasiones un modelo lineal es insuficiente para explicar un fenómeno: la variable objetivo puede no depender linealmente de una variable explicativa. Aunque este tipo de modelos no suelen abordarse en cursos introductorios (ni siquiera de estadística), es ilustrativo mostrar cómo pueden aplicarse de manera sencilla en R.
En el siguiente trozo de código, vamos a cargar un conjunto de datos y ajustador un modelo lineal idéntico al que hubiésemos obtenido con la función lm, aunque usando la función gam del paquete mgcv.
library(mgcv)
pisa <- read.table("data/pisasci2006.csv", header = T, sep = ",")
mod.gam.0 <- gam(Overall ~ Income, data = pisa)
summary(mod.gam.0)
Family: gaussian
Link function: identity
Formula:
Overall ~ Income
Parametric coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 204.32 35.37 5.777 4.32e-07 ***
Income 355.85 46.79 7.606 5.36e-10 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
R-sq.(adj) = 0.518 Deviance explained = 52.7%
GCV = 1504.5 Scale est. = 1448.8 n = 54Ejercicio 12.20 Compara los resultados del modelo anterior con los que se obtendrían con lm.
Lo interesante es que gam permite introducir términos especiales para modelar efectos no lineales. Por ejemplo, en estos datos, los ingresos. El gráfico generado ilustra el impacto (no lineal) del ingreso sobre la variable objetivo.
mod.gam.1 <- gam(Overall ~ s(Income, bs = "cr"), data = pisa)
summary(mod.gam.1)
Family: gaussian
Link function: identity
Formula:
Overall ~ s(Income, bs = "cr")
Parametric coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 470.444 4.082 115.3 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Approximate significance of smooth terms:
edf Ref.df F p-value
s(Income) 6.895 7.741 16.67 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
R-sq.(adj) = 0.7 Deviance explained = 73.9%
GCV = 1053.7 Scale est. = 899.67 n = 54plot(mod.gam.1)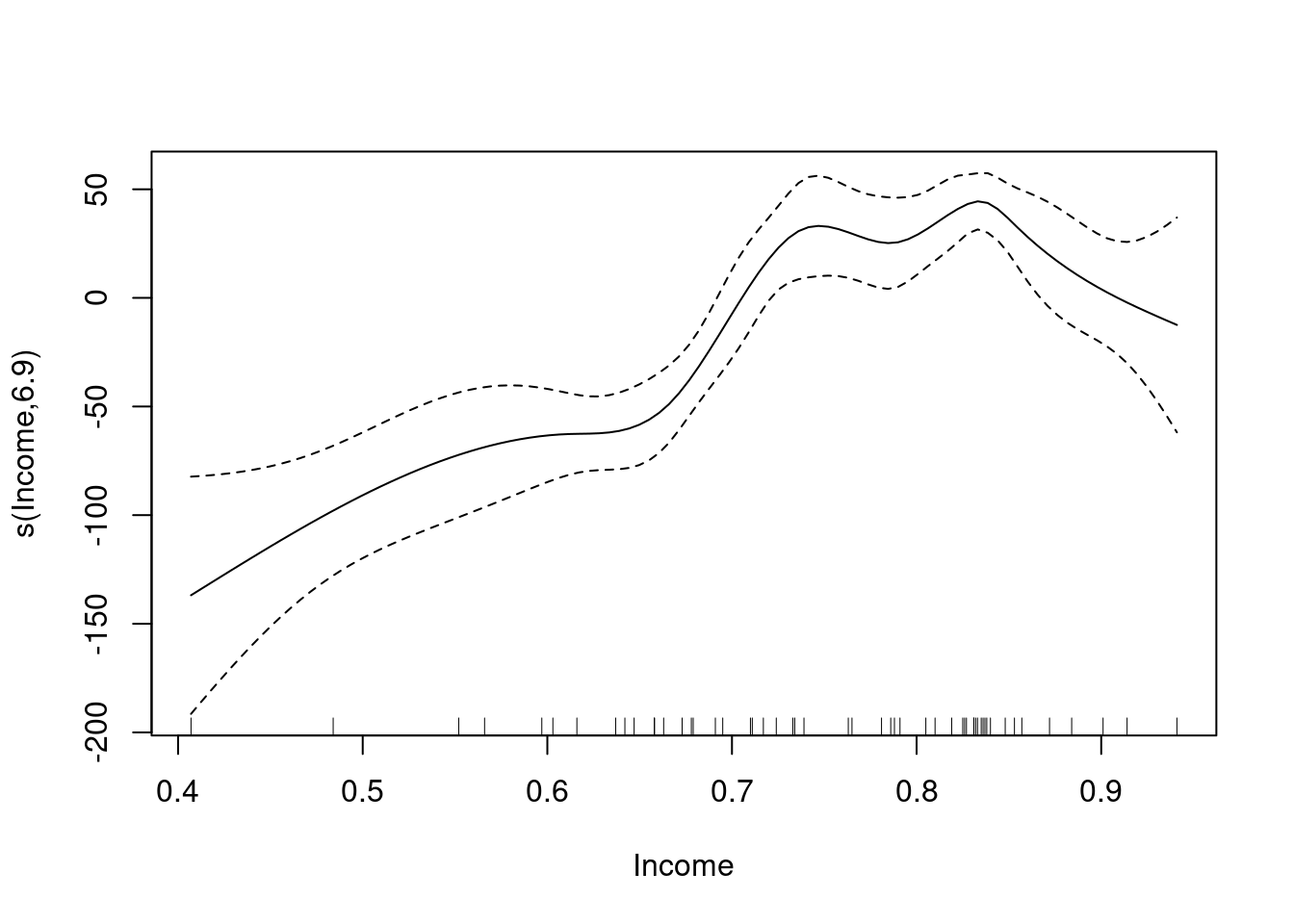
Ejercicio 12.21 Usa predict con ambos modelos para estimar su correspondiente error cuadrático medio (la media de la diferencia entre los valores reales y estimados al cuadrado).
12.8 Clústering con k-medias
La función kmeans de R aplica el algoritmo de las k-medias para encontrar grupos de observaciones similares. Puedes visitar https://www.datanalytics.com/2016/04/18/visualizacion-de-k-medias-y-dbscan/ para ver una animación que muestra cómo funciona el algoritmo.
Vamos a ilustrar el uso de este algoritmo con R usando iris para tratar de agrupar los registros en tres grupos por sus variables numéricas (una limitación de k-medias):
dat <- iris[,1:4]
res <- kmeans(dat, 3)Ejercicio 12.22 Investiga el objeto res. Busca en particular el grupo al que el el algoritmo asocia cada observación.
Ejercicio 12.23 Compara los clústers obtenidos con las especies (conocidas). Nota: puede servirte hacer table(iris$Species, res$cluster).
Ejercicio 12.24 Repite el ejercicio anterior 3 o 4 veces: ¿obtienes los mismos (o equivalentes) resultados cada vez?
Ejercicio 12.25 Haz lo mismo pero usando 4 clústers.
12.9 Resumen y referencias
12.9.1 Árboles
En este capítulo hemos usado árboles en un problema de clasificación. Los árboles tienen una historia que se remonta a finales de los años setenta y fueron presentados en sociedad en el libro de 1984 Classification and Regression Trees, de Leo Breiman y otros coautores. Desde entonces se han creado muchas versiones de los árboles (CART, C4.5, etc.). Los árboles originales, los descritos en el libro anterior, están implementados en el paquete rpart de R. Nosotros, sin embargo, hemos usado los de party, que están basados en desarrollos teóricos posteriores.
Los árboles, en cualquiera de sus versiones, tienen las características indicadas en este capítulo: son simples, excesivamente simples y su poder predictivo es limitado, pero son fáciles de interpretar. Existen dos estrategias para mejorar el poder predictivo de los árboles. La primera es crear muchos de ellos y promediarlos. Es la que siguen los bosques aleatorios sugeridos más arriba. La segunda es crear iterativamente listas de árboles de manera que el i-ésimo corrija los errores cometidos por los anteriores. Es la estrategia subyacente a xgboost y sus versiones.
En ambos casos se pierde en gran medida la interpretabilidad de los modelos. Sin embargo, como contrapartida, tanto los bosques aleatorios como los basados en la técnica del boosting permiten construir modelos con un poder predictivo muy alto.
12.9.2 Pruebas de hipótesis
En R están implementadas infinidad de pruebas estadísticas: t.test, wilcox.test, prop.test, etc. De hecho, la inmensa mayoría de las que se enseñan en los cursos de introducción a la estadística. Sin embargo, R nos permite ir más allá de las limitaciones inherentes a este tipo de pruebas. Por ejemplo, tal y como hemos ilustrado en esta sección, nos permite crear nuestras propias pruebas mediante remuestreos.
Pero también, y aunque no nos hemos ocupado de eso, también nos permite subsumir pruebas estadísticas en modelos estadísticos que permiten considerar fuentes alternativas de información, i.e., el efecto confusor de otras variables observadas sobre el fenómeno. Y esto tanto bajo un punto de vista estrictamente frecuentista como desde otro, más moderno, bayesiano que da respuesta a los problemas metodológicos asociados a las pruebas de hipótesis, los p-valores, los errores de tipo I y II, etc.
12.9.3 Modelos lineales y sus extensiones
El modelo lineal ilustrado en esta sección tiene una larga historia y aunque hay pocos contextos en los que hoy en día sea la opción de modelado preferible, mucha de la estadística y la ciencia de datos moderna consiste en generalizaciones suyas. En esta sección hemos explorado algunas de ellas, como el modelo logístico (como ejemplo de los llamados modelos lineales generalizados) y los modelos lineales generalizados (GAM), pero podríamos haber tratado las regresiones penalizadas (ridge, lasso, elasticnet, etc.).
Una ventaja de R es que proporciona una interfaz relativamente homogénea y previsible para todos estos tipos de modelos: todos cuentan con una función predict, summary, etc.
12.9.4 Clústering
En esta sección hemos presentado el algoritmo de clústering más utilizado, k-medias. No obstante, existen alternativas como como las implementadas en el paquete cluster. Una alternativa cada vez más popular a los métodos clásicos anteriores es DBSCAN (véase https://cran.r-project.org/web/packages/dbscan/index.html).
Los conceptos de función de densidad, de probabilidad, etc. son muy importantes, aunque no en el resto del libro. Si estás familiarizado con ellos, te servirá lo que sigue; si no, puedes ignorarlo en una primera lectura.↩︎
Es muy importante no utilizar los datos usados para validar modelos en el ajuste de los mismos.↩︎
Aunque en algunos casos puede admitir algunos más↩︎
La manera excede el alcance del curso.↩︎