La falacia del fiscal (pero con frecuencias naturales)
No sé si alguien conoce la historia de Sally Clark. Fue condenada por el asesinato de sus dos hijos. Ambos padecieron, según ella, el síndrome de la muerte súbita del lactante. La probabilidad, sin embargo, de que sus dos hijos lo padecieran (supuesto que son eventos independientes, i.e., que no hay, por ejemplo, factores genéticos comunes) era muy baja: una de 73 millones. Por eso la enchironaron.
Pero, ¿qué es 1 / 73e6? Eso es $latex P(D|I)$, es decir, la probabilidad del suceso (los datos) condicionada a la inocencia de Sally. Sin embargo, la probabilidad que tiene que tener encuenta un juez no es esa sino $latex P(I|D)$, es decir, la probabilidad de ser inocente a la vista de los datos.
Para pasar de $latex P(D|I)$ a $latex P(I|D)$ hay que aplicar, obviamente, el teorema de Bayes:
$$ P(I|D) = P(D|I) \frac{P(I)}{P(D)}$$
Se puede suponer que $P(I)$, la probabilidad de que alguien sea, en principio, inocente de asesinar críos, es prácticamente 1. Por otro lado, $latex P(D) = P(D|I) P(I) + P(D|C) P(C)$, es decir, la probabilidad de que dos niños mueran inexplicablemente es la suma de la probabilidad de que mueran por causas naturales siendo inocente la madre y la de que mueran cuando esta es culpable. Se puede argumentar que esa suma es en este caso, aproximadamente, solo un poco mayor que $latex P(C)$:
- $latex P(I)$ es prácticamente uno
- por lo tanto, $latex P(D|I) P(I)$ viene a ser $latex P(D|I) P(I)$
- además, $latex P(D|C)$ es también casi uno
Así que
$$ P(I|D) = P(D|I) \frac{P(I)}{P(D)} \sim \frac{P(D|I)}{P(C)}$$
Sabíamos ya que $latex P(D|I)$ es una cantidad pequeña, 1/73e6. Pero también lo es $latex P(C)$, la probabilidad de que alguien sea culpable. La culpabilidad de Sally está mucho menos clara bajo este punto de vista.
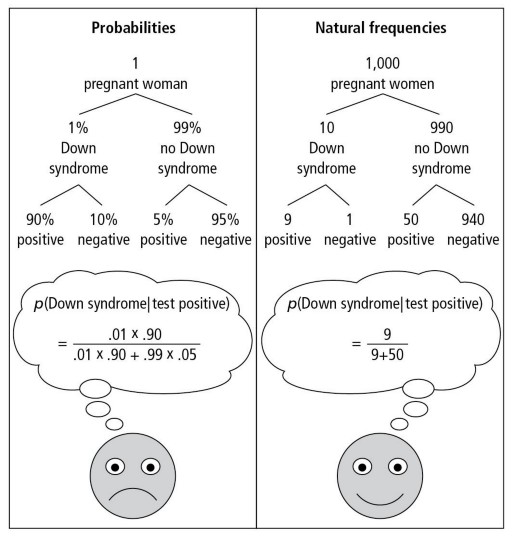
De todos modos, el teorema de Bayes confunde a profanos y no profanos. No tengo claro que todo el mundo que haya leído hasta este punto haya quedado convencido con el argumento anterior. Y no lo digo yo, sino expertos en el arte de divulgar información probabilística (y de riesgos) como dos de los héroes de esta bitácora: D. Spiegelhalter y G. Gigerenzer, que abogan, más que por la aplicación del teorema de Bayes, por las frecuencias naturales.
Imaginad una lista de 73 millones de puntos verdes: son mujeres que han tenido dos hijos. Casi todos los puntos son verdes. Pero hay uno azul y unos pocos rojos. El azul es el caso en el que ha habido una doble muerte súbita. Los rojos son los casos en que mujeres desequilibradas han asesinado a sus hijos.
A la vista de dos cadáveres de neonatos, la probabilidad de que la madre sea inocente (nuestra $latex P(I|D)$) es la razón entre el número de puntos azules (uno) y el de puntos rojos más uno (el azul).
¿Cuántos puntos rojos hay? No lo sabemos. Pero lo que está claro es que la probabilidad está muy lejos de la 1/73e6 que llevó a Sally a la cárcel.