Python y R: una perspectiva markoviana
Hoy he visto
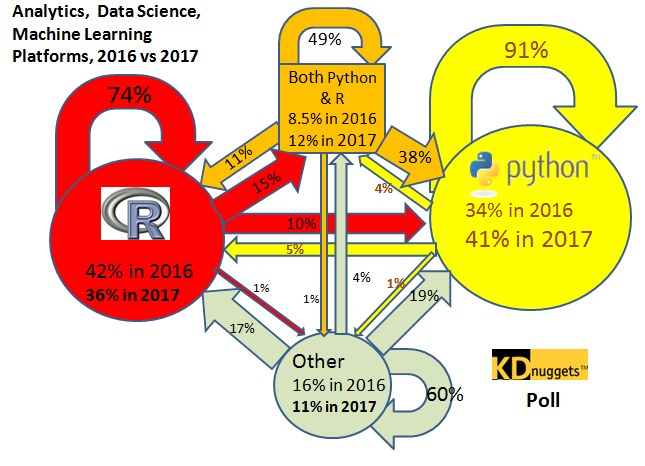
aquí y he escrito
m <- matrix(c(74, 15, 10, 1, 11, 50, 38, 1,
5, 4, 90, 1, 17, 4, 19, 60),
4, 4, byrow = TRUE)
m <- m / 100luego
m %*% m %*% m %*% m %*% m %*% m %*% m %*% m %*% m %*% m %*% m %*% m %*% m%*% m%*% m%*% m%*% m%*% m%*% m %*% m %*% m %*% m %*% m %*% m %*% m %*% m %*% m %*% m %*% m %*% m %*% m%*% m%*% m%*% m%*% m%*% m%*% m
# [,1] [,2] [,3] [,4]
#[1,] 0.1926676 0.1133218 0.6696203 0.02439024
#[2,] 0.1926647 0.1133206 0.6696245 0.02439024
#[3,] 0.1926638 0.1133202 0.6696258 0.02439024
#[4,] 0.1926675 0.1133218 0.6696205 0.02439025y finalmente
res <- eigen(t(m))
res$vectors[,1] / sum(res$vectors[,1])
#[1] 0.19266473 0.11332059 0.66962444 0.02439024Aquí dice por qué.

