Sobre la función de riesgo en el análisis de la supervivencia

Tienes una función de supervivencia

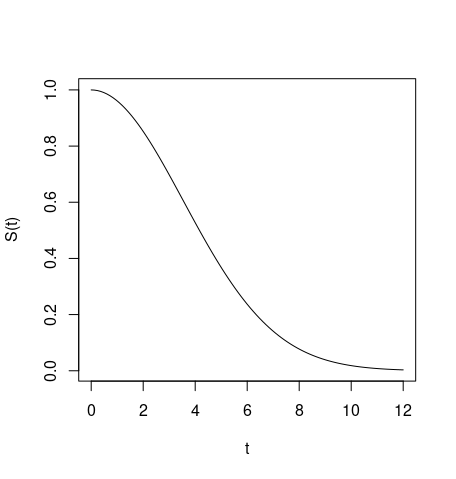
y piensas que es posible aproximarla usando segmentos de exponencial usando primero una rejilla gruesa,

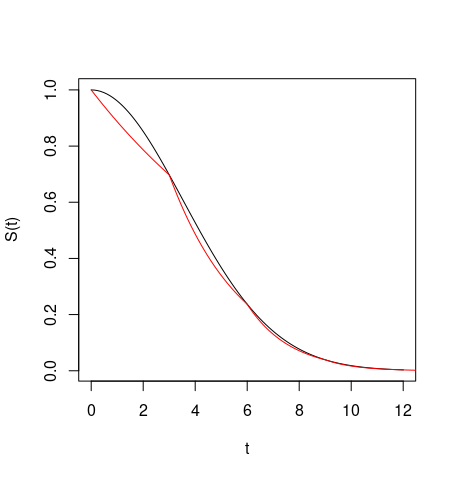
y luego cada vez más fina,

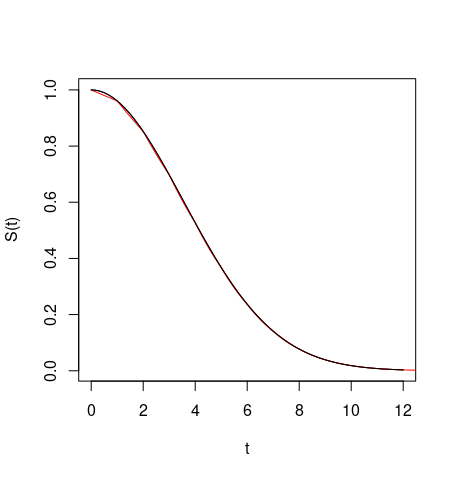
hasta que sean indistinguibles.

Las distintas aproximaciones son

$\hat{S}(t) = \exp\left(-\sum_{i \le n} \lambda_i \Delta - \lambda_n (t - t_n)\right)$

donde $n$ es el índice del intervalo que contiene a $t$ los $\lambda_i$ son los coeficientes en los segmentos de exponencial. Esa expresión que converge a

$S(t) = \exp\left(-\int_0^t \lambda(x) dx\right)$

y $\lambda(t) = -S^\prime(t) / S(t)$ como no es necesario demostrar.

Ah, y sí, $\lambda(t)$ es la función de riesgo.

Coda: entre otras cosas, queda evidenciado que la función de riesgo del decaimiento exponencial es constante.

PD: Por si alguien quiere jugar con el código que ha servido para pintar lo anterior,

S <- function(x) 1 - pweibull(x, 2, 5)

from = 0
to = 12

curve(S(x), from = from, to = to, xlab = "t", ylab = "S(t)")

incr <- 1

for(init in seq(from, to, by = incr)){
    a <- S(init)
    b <- S(init + incr)
    lambda <- - log(b / a) / incr
    curve(S(init) * exp(-lambda * (x - init)),  
          from = init, to = init + incr, 
          col = "red", add = T)
}


curve(S(x), from = from, to = to, xlab = "t", ylab = "S(t)", add = T)

Un comentario sobre “Sobre la función de riesgo en el análisis de la supervivencia”