CRPS

Hoy toca hablar del CRPS, o continuous ranked probability score, que es un tipo particular de scoring y que se usa para lo que se usan los scorings: comparar modelos y predicciones.

Imaginemos que alguien quiere predecir un determinado valor y que como no es un patán, tiene la gentileza de proporcionar la distribución del valor esperado (p.e., una $N(a, b)$). Resulta que el valor observado es $x_o$.

¿Cómo de buena es esa predicción? En principio, cuando más probable sea $x$ en términos de la función de probabilidad de la predicción, mejor será dicha predicción. Así que $p(x_o)$ —donde $p$ es la función de densidad de la predicción— podría ser un buen scoring. En la práctica se usa una versión de la anterior, $\log(p(x_o))$, pero viene a ser lo mismo.

Otra manera sería comparar la función de probabilidad de la predicción y la empírica de la observación. La primera es

$$F(x) = \int_{-\infty}^x p(y) dy$$

y la segunda, $F_e(x) = 0$ si $x < x_0$ y $F_e(x) = 1$ si $x \ge x_0$.

Las dos funciones (suponiendo que la predicción es una $N(1, .5)$ y que el valor observado es 1.4) son, gráficamente,

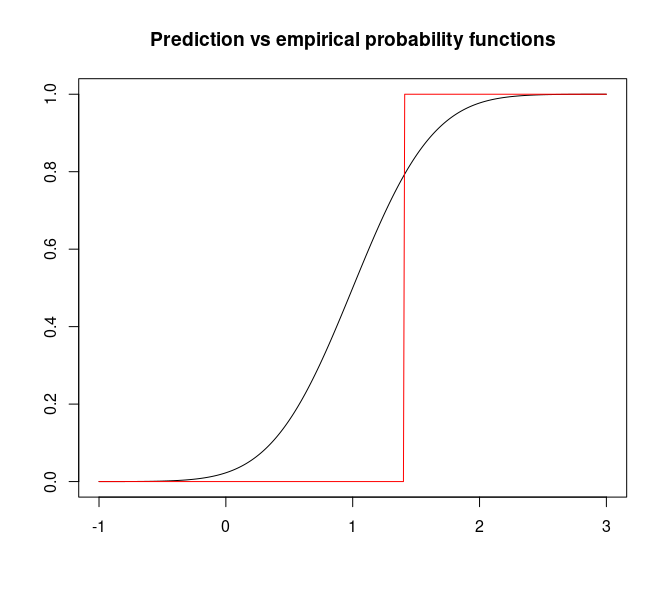
La distancia cuadrática (o en norma $l_2$) entre ambas funciones, i.e.,

$$\int_{-\infty}^\infty (F(x) - F_e(x))^2 dx$$

es una medida del error cometido.

En esto resuenan ecos del teorema de Givenko-Cantelli: si en lugar de solo una observación, tenemos muchas, la distancia entre la función de distribución empírica (construida no solo con una observación sino con muchas) y la verdadera tiende a cero.

Así que el CRPS es Gilvenko-Cantelli con $n = 1$, si se quiere.

Podría seguir diciendo que hay software para ajustar modelos usando el CRPS en lugar de otras métricas, como el RMSE, etc., pero tengo que ir a cenar.