Coeficientes "no identificables": un ejemplo y sus consecuencias

Hoy voy a abundar sobre el modelo 3PL que ya traté el otro día. En particular voy a contrastar críticamente varios modelos alternativos sobre los mismos datos.

I.

El modelo que implementé (aquí) puede describirse así:

$$r_{ij} \sim \text{Bernoulli}(p_{ij})$$ $$p_{ij} = p(a_i, d_j, …)$$ $$a_i \sim N(0, 1)$$ $$d_j \sim N(0, 1)$$ $$\dots$$

donde

$$p = p(a, d, \delta, g) = g + \frac{1 - g}{1 + \exp(-\delta(a- d))}$$

y $a_i$ y $d_j$ son la habilidad del alumno $i$ y la dificultad de la pregunta $j$ respectivamente. Nótese además cómo en $f$ estas dos variables intervienen solo a través de su diferencia, $a - d$.

El modelo así planteado viene a significar lo siguiente:

• Hay una serie de alumnos que tienen una habilidad que en principio y para la población general tiene una distribución normal estándar. Puede pensarse en el IQ o, en casos más concretos, los conocimientos de dibujo técnico de las población global de alumnos de segundo de ingeniería de caminos.
• Que una pregunta tenga una dificultad de 1.5 significa que un alumno con habilidad de 1.5 la respondería correctamente el 50% de las veces (si no hubiese cierta probabilidad indicada por $g$ de acertar al azar).

Después del examen, las habilidades de los alumnos, que en principio eran vagas (una $N(0, 1)$) se van concretando y la estimación de la habilidad de un alumno que lo haga relativamente bien puede acabar teniendo una distribución similar a una $N(1.7, 0.2)$.

Lo mismo ocurre con las preguntas: en principio, no son ni fáciles ni difíciles, pero el desempeño de los estudiantes afina la estimación que se pueda hacer de su grado de dificultad.

Entiendo que para construir exámenes estandarizados o tests sicométricos hay que probarlos contra poblaciones de sujetos normales (i.e., globalmente $N(0,1)$) para estimar los parámetros de las preguntas. Después, las pruebas se pueden aplicar a otros conjuntos de sujetos distintos y potencialmente variopintos.

II.

Uno puede introducir variaciones el el modelo anterior. Por ejemplo,

$$r_{ij} \sim \text{Bernoulli}(p_{ij})$$ $$p_{ij} = f(a_i, d_j, …)$$ $$a_i \sim N(\mu_a, \sigma_a)$$ $$d_j \sim N(0, 1)$$ $$\dots$$ $$\mu_a \sim N(0, 2)$$ $$\sigma_a \sim \Gamma(1, 1)$$

Este modelo está sugiriendo que tal vez la población de partida tiene un sesgo respecto a la población base. Si $\mu_a > 0$ significativamente, podríamos decir que los estudiantes en cuestión son globalmente mejores que la media.

Variaciones bastante evidentes de este modelo nos permitirían comparar grupos (a lo PISA), etc.

Este modelo tiene interés cuando nos importan menos los estudiantes individuales que su comportamiento global.

III.

El dual de II es

$$r_{ij} \sim \text{Bernoulli}(p_{ij})$$ $$p_{ij} = f(a_i, d_j, …)$$ $$a_i \sim N(0, 1)$$ $$d_j \sim N(\mu_d, \sigma_d)$$ $$\dots$$ $$\mu_d \sim N(0, 2)$$ $$\sigma_d \sim \Gamma(1, 1)$$

al que se pueden aplicar, mutatis mutandis, los comentarios del bloque anterior.

IV.

Sin embargo, la combinación de II y III,

$$r_{ij} \sim \text{Bernoulli}(p_{ij})$$ $$p_{ij} = f(a_i, d_j, …)$$ $$a_i \sim N(\mu_a, \sigma_a)$$ $$d_j \sim N(\mu_d, \sigma_d)$$ $$\dots$$ $$\mu_a \sim N(0, 2)$$ $$\sigma_a \sim \Gamma(1, 1)$$ $$\mu_d \sim N(0, 2)$$ $$\sigma_d \sim \Gamma(1, 1)$$

es sumamente problemática. Este modelo, sobre todo si las prioris son laxas, deja flotar simultáneamente $\mu_a$ y $\mu_d$. Pero, recuérdese cómo para $p$ solo la diferencia entre $a$ y $d$ es relevante. Por lo tanto, al ajustar el modelo, una simulación donde $\mu_a = 0$ y $\mu_d = 2$ tiene la misma verosimilitud que otra en la que $\mu_a = 5$ y $\mu_d = 7$: su diferencia es siempre $-2$.

Es decir, salvo que sus prioris sean muy estrictas y las anclen en valores casi fijos, se puede vaticinar que la correlación entre las posteroris de $\mu_a$ y $\mu_d$ sea muy grande. Y, en efecto,

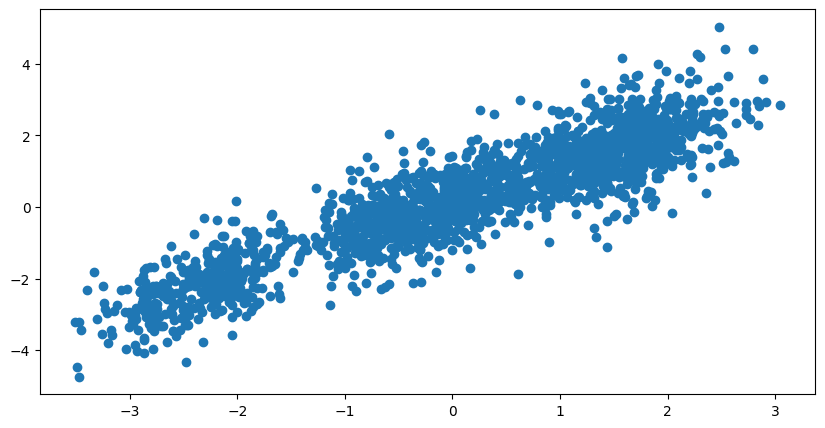
Es decir, $\mu_a$ y $\mu_d$ por sí solas no significan nada. Traducido a términos no técnicos, no sabríamos si los estudiantes lo hicieron muy mal porque el examen era muy difícil o que el examen era muy sencillo pero los estudiantes no estaban preparados. Si desconocemos ambas premisas, ninguna puede establecerse.

La incertidumbre asociada a los parámetros en cuestión se propaga por el resto de los parámetros de interés —ejercicio para el lector: ¿qué pasará con la incertidumbre de las abilidades individuales de los alumnos?— y no queda claro qué es lo que aprende el modelo o qué conclusiones puedan extraerse de él.

V.

Daría para otra entrada paralela a esta discutir, además, el efecto de la discriminación (el parámetro $\delta$ del modelo). Este parámetro se llama discriminación porque mide en qué medida una pregunta es capaz de diferenciar estudiantes que saben la respuesta de los que no: hay preguntas muy fáciles –por ejemplo, ¿cuál es el rango de la matriz de dimensión $1\times 1$ $(7)$?— que distinguen muy fácilmente a aquellos que saben qué es una matriz y cuál es su rango de los que no.

Volviendo a la formulación de $p$,

$$p(a, d, \delta, g) = g + \frac{1 - g}{1 + \exp(-\delta(a- d))}$$

se observa cómo $\delta$ solo tiene un efecto de escala sobre la diferencia $(a- d)$. Así que la verosimilitud no cambia si se multiplica $\delta$ por 10 y se dividen $a$ y $d$ por 10. Eso significa que para que el modelo sea identificable, hay que anclar las varianzas de $a$ y $d$ de partida. Es decir, que las prioris de $\sigma_a$ y $\sigma_d$ deberían ser muy estrechas (o, como en el primer modelo, fijas).

A modo de resumen

Construir un modelo es como construir un reloj: se puede hacer de muchas maneras, con diferentes conjuntos de piezas y en distintas configuraciones. Pero todas tienen un porqué y una función que, por supuesto, son legibles. A partir de esta lectura podemos identificar potenciales problemas y sus soluciones. Como en el en caso tratado más arriba.