(Estadística y fraude electoral) vs (fraude electoral y fraude estadístico)

Hay un blog que conoció mejores tiempos, lleva varios años en caída libre y estoy por quitar de mi lista de RSS: NadaEsgratis. Para aprender de lo que trata hay mejores sitios. Y de lo único que informa, el lastimoso estado de la disciplina en cuestión en España, es agua sobre mojado.

Pero de vez en cuando inspira entradas. Por ejemplo, Estadística y fraude electoral: lo que el teorema central del límite nos revela acerca del régimen de Putin, de Manuel Bagues.

[Que Manuel Bagues se dedique a la economía del trabajo debería pasar a la lista de aptónimos, junto con la del botánico profesor Plant, etc.]

Dice Bagues:

Examinemos los resultados del referéndum que tuvo lugar en Junio de 2020 para eliminar el límite de mandatos, permitiendo la reelección de Putin hasta el año 2036. Si echamos un ojo a los resultados electorales por colegio electoral, llama la atención que el porcentaje de votos a favor de la reforma propuesta por Putin tiende a ser prácticamente idéntico en muchos colegios electorales de cada distrito electoral. Por ejemplo, en el distrito de Akushinsky, que cuenta con unos 52 colegios electorales de unos 500 votantes cada uno, votó a favor de la propuesta de Putin exactamente el 93.0% de los votantes en la práctica totalidad de los colegios electorales.

Luego, muestra el siguiente gráfico:

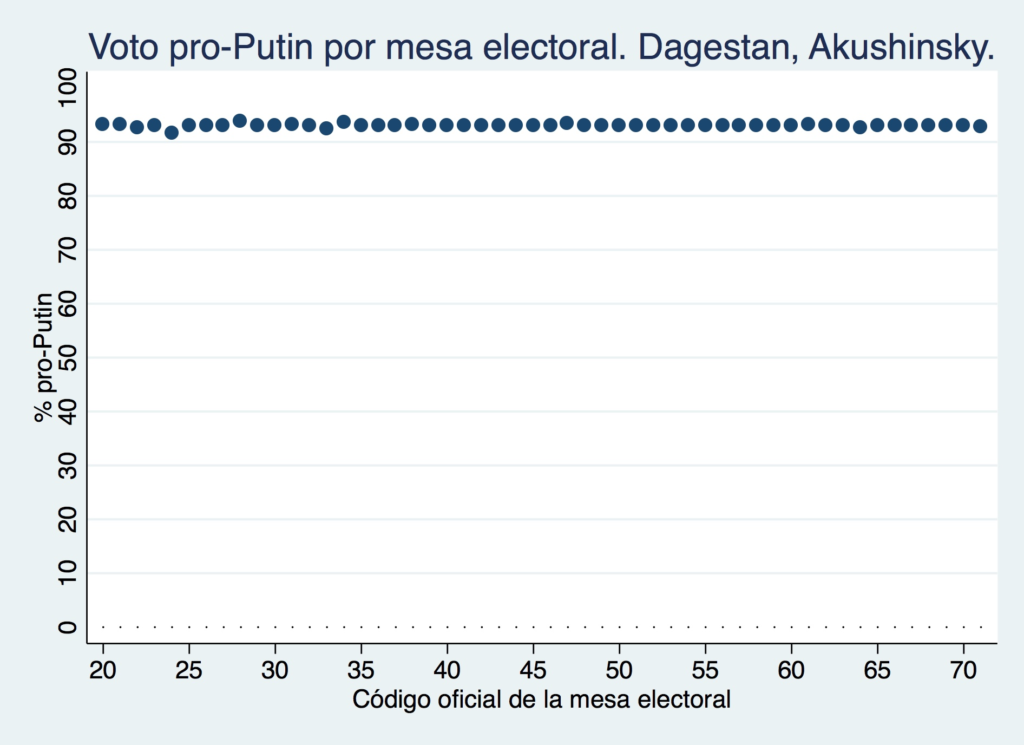
Y finaliza la discusión demostrando que la varianza es mucho menor de la esperada de dos maneras distintas:

• Mediante una simulación.
• Mediante la aplicación del teorema central del límite, según el cual, dice, los votos recibidos por Putin en los distintos colegios electorales deberían seguir una distribución normal con una desviación estándar igual a

Es decir, un 1.1% en lugar del 0.3% de los datos. QED.

Pero no, el análisis es incorrecto. Y no me refiero (solo) al hecho de que no contemple la distribución de los valores posibles de la desviación estándar de la muestra —para calcular propiamente el p-valor correspondiente al valor observado 0.3%—. O Bagues es un trilero y nos la ha clavado subrepticiamente o ha cometido un error inadvertidamente. El problema es que si uno baja los datos, comprobará que de los más de 2700 colegios electorales en Rusia y los ordena por la desviación estándar del resultado por urna, el de Akushinsky, el del ejemplo, es el primero (en realidad, es el quinto, pero los cuatro anteriores son minúsculos; deben de corresponder a lugares perdidos de Kamchatka donde apenas hay cuatro cabañas de leñadores). Akushinsky no se ha elegido al azar. Akushinsky se ha elegido porque es un extremo de la distribución. Bien podría ser, incluso, un outlier.

Que debe ser estudiado como tal, no como un lugar representativo. Es decir, habría que modificar el análisis, habría que simular la desviación estándar del lugar donde menos varianza hay de 2700 y, también, realizar los cambios pertinentes en la aplicación del TCL, si es que procede siquiera.

Hay publicados por ahí varios análisis de esas elecciones que también señalan la alta probabilidad de fraude electoral, obviamente examinando factores distintos. Es muy posible además que, en Akushinsky, algún fiel funcionario sin mucha imaginación haya fabricado esos números de los que hablamos. Pero por muy malvado que sea Putin, por fehacientes que resulten las evidencias de fraude, no todo vale. Al menos, para quien suscribe.