¿Cómo se interpretan los resultados de estas regresiones

Esta entrada trata sobre las aparentes contradicciones que surgen cuando se comparan las regresiones $y \sim x$ y $x \sim y$. En particular, aqui se muestran

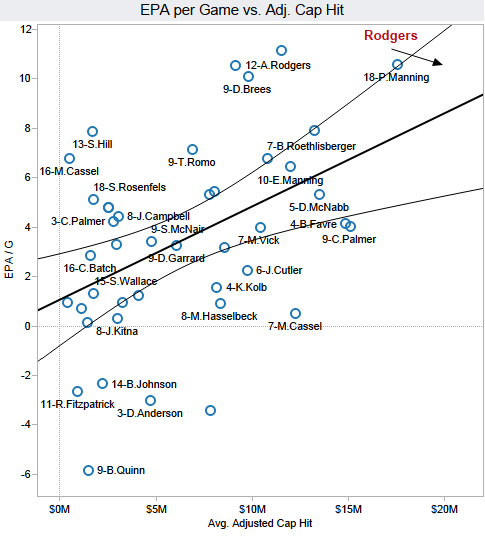
y

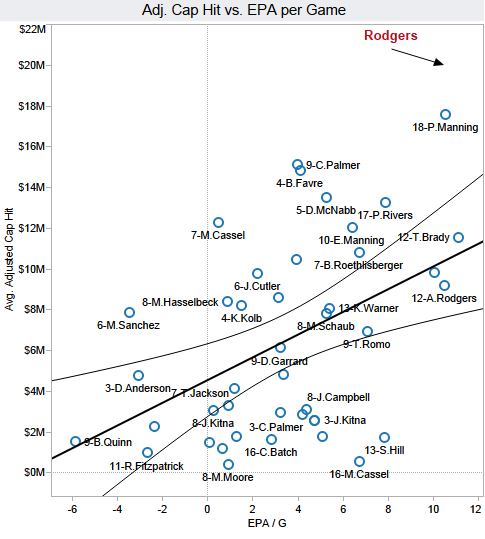
que vienen a decir:

• El tal Rodgers rinde por encima de lo que se espera para su salario.
• Para lo que rinde, gana demasiado.

Lo cual, a pesar de lo contradictorio, no es un fenómeno extrañísimo. Si uno hace

n <- 100
x <- rnorm(n)

a <- .3
b <- .5
y <- a * x + b + 0.1 * rnorm(100)

reg1 <- lm(y ~ x)
reg2 <- lm(x ~ y)

which.1 <- y > predict(reg1, data.frame(x = x))
which.2 <- x > predict(reg2, data.frame(y = y))
tmp <- cbind(which.1, which.2)
tmp <- which(tmp[,1] & tmp[,2])

ab <- coef(reg2)

plot(x, y)
abline(reg1, col = "blue")
abline(b = 1/ ab[2], a = - ab[1] / ab[2], col = "green")

points(x[tmp], y[tmp], col = "red", pch = 16)

puede obtener tantos gráficos de la forma

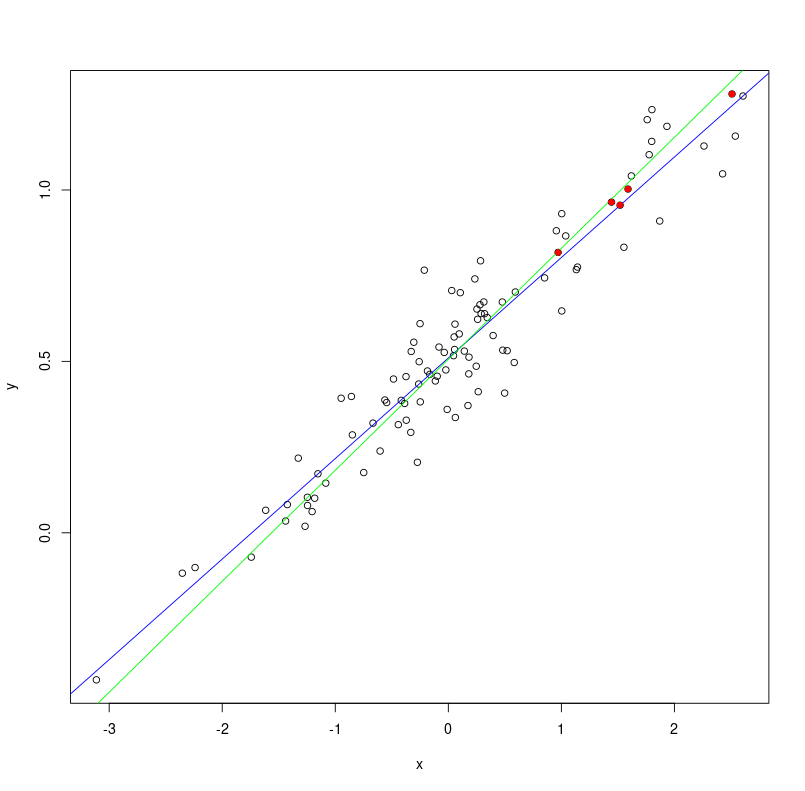
como uno quiera; en todos ellos, los puntos sólidos rojos son los rodgers.

Por si alguien no la conoce, enlazo la discusión de Andrew Gelman sobre el asunto.

La mía es más o menos así: este ejemplo pone de manifiesto un bug de la regresión lineal que uno puede convertir en feature cuando lo que le interesa es invertir el significado de unos números. Dicho de otra manera, dado que hoy en día está de moda despejar (como en una ecuación) la figura del relator y hacer que sean los propios números los que armen las historias, ese relator oculto entre las bambalinas puede —no siempre se da la feliz circunstancia, como evidencian los gráficos anteriores— tener la opción de elegir entre $y \sim x$ o $x \sim y$ para que los corolarios sean del agrado de quien ha de pagarle la nómina.