R

Si se puede hacer para Japón, también se puede hacer para España:

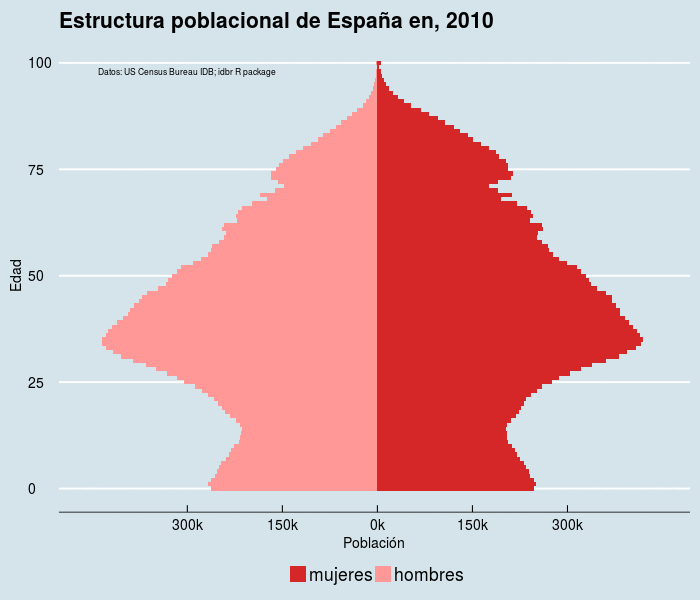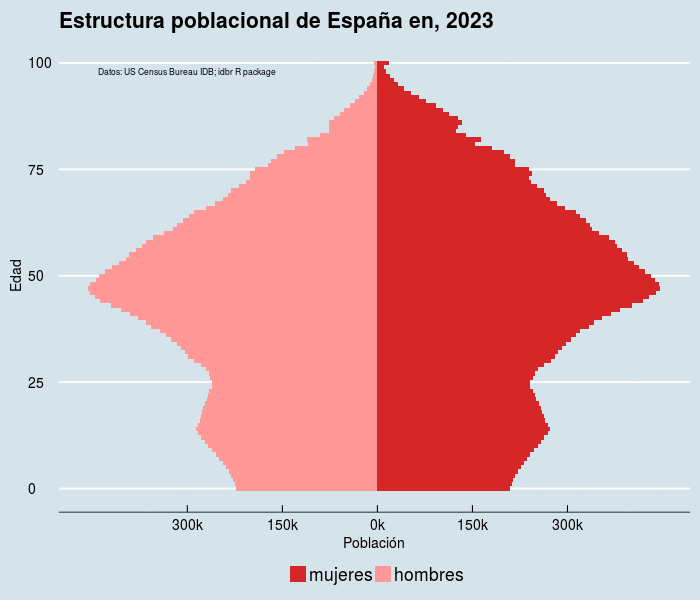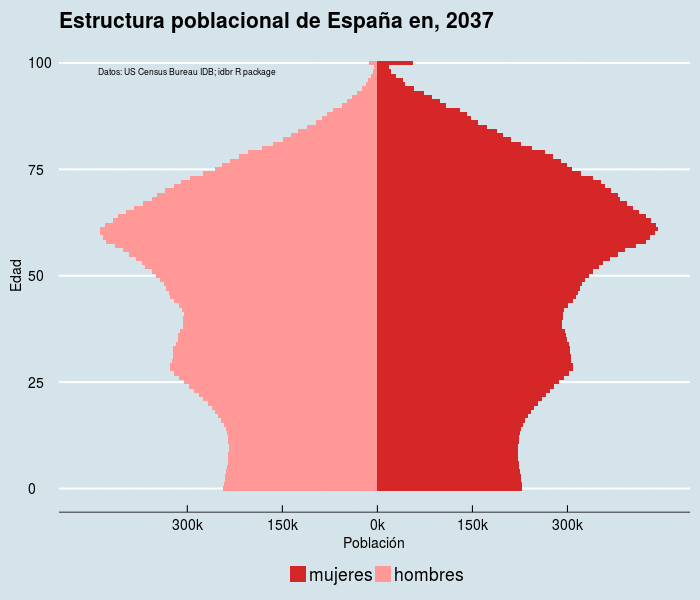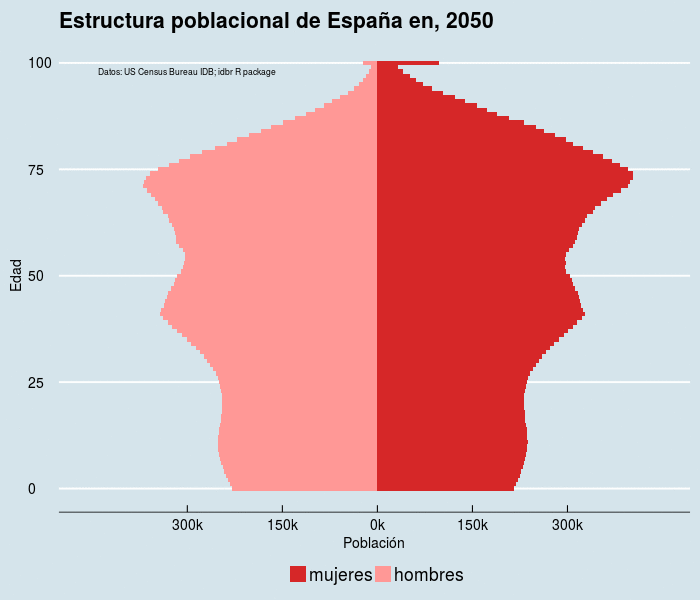
El código,

library(idbr)
library(ggplot2)
library(animation)
library(ggthemes)

idb_api_key("pídela en https://www.census.gov/data/developers/data-sets/international-database.html")

male <- idb1('SP', 2010:2050, sex = 'male')
male$SEX <- "hombres"
male$POP <- -male$POP

female <- idb1('SP', 2010:2050, sex = 'female')
female$SEX <- "mujeres"

spain <- rbind(male, female)

saveGIF({

  for (i in 2010:2050) {

    title <- as.character(i)

    year_data <- spain[spain$time == i, ]

    g1 <- ggplot(year_data, aes(x = AGE, y = POP, fill = SEX, width = 1)) +
      coord_fixed() +
      coord_flip() +
      annotate('text', x = 98, y = -300000,
                label = 'Datos: US Census Bureau IDB; idbr R package', size = 3) +
      geom_bar(data = subset(year_data, SEX == "mujeres"), stat = "identity") +
      geom_bar(data = subset(year_data, SEX == "hombres"), stat = "identity") +
      scale_y_continuous(breaks = seq(-300000, 300000, 150000),
                          labels = paste0(as.character(c(seq(300, 0, -150), c(150, 300))), "k"),
                          limits = c(min(spain$POP), max(spain$POP))) +
      theme_economist(base_size = 14) +
      scale_fill_manual(values = c('#ff9896', '#d62728')) +
      ggtitle(paste0('Estructura poblacional de España en, ', title)) +
      ylab('Población') +
      xlab('Edad') +
      theme(legend.position = "bottom", legend.title = element_blank()) +
      guides(fill = guide_legend(reverse = TRUE))

    print(g1)

  }

}, movie.name = 'spain_pyramid.gif', interval = 0.1,
    ani.width = 700, ani.height = 600)

Pues sí, acabo de enterarme de que se organiza la tal cosa. Toda la información, escasa de momento, aquí.

CatastRo es un paquete de R para explotar la API del Catastro que fue realizado por un alumno mío de la UTAD, Ángel Delgado, como proyecto de fin de máster.

Ahora, una vez integrado en rOpenSpain, toca transformarlo de un proyecto académico en un paquete útil y práctico. Vamos, exponerlo al proceloso piélago del uso para que le crujan las costuras y ver cuáles son las mejoras más pertinentes.

Así que estáis todos invitados a probar el código, verificar que la documentación documenta, que los ejemplos ejemplifican, etc. y, por supuesto, a notificar cualquier cosa que observéis abriéndole un issue al paquete, como poco.

Cayeron en mis manos unos datos que no puedo publicar, pero me atreveré a presentar algunos resultados anonimizados. Se trata de una tabla de puntuaciones numéricas (18 en total, cada una en su columna) proporcionadas por unos cuantos centenares de sujetos (filas). Era de interés un estudio cualitativo de las posibles relaciones de dependencia entre las variables.

La manera más rápida de comenzar, un heatmap(cor(dat)), para obtener

Y luego PCA y todas esas cosas.

Con motivo de fin de año se ha hablado de fallecidos en accidentes de tráfico como por ejemplo en El Mundo o en El País. Y sí, parece que el número observado de muertos ha aumentado.

Lo cual es mucho menos relevante de lo que se da a entender. Si tiras una moneda al aire 100 veces y sacas 48 caras y luego repites el experimento, podrías sacar 53 (y habría aumentado el número observado de caras) o 45 (y habría disminuido). Lo relevante es si ha cambiado o no la probabilidad de cara de la moneda. De lo cual, y volviendo al caso de la siniestralidad, ya me ocupé en su día.

Imagínate que quieres estabilizar la varianza (¡para qué!) de una distribución de Poisson. Los libros viejunos te dirán que saques la raíz cuadrada de tus valores.

Si en lugar de mirar en libros viejunos prestas atención a tus propios ojos, harás algo parecido a:

lambdas <- -10:10
lambdas <- 2^lambdas
res <- sapply(lambdas,
    function(lambda) sd(sqrt(rpois(1e5, lambda))))

para obtener

y averiguar dónde funciona y dónde no.

Si usas la transformación $latex f(x) = x^{2/3}$, como recomiendan en cierto artículo que no viene a cuento identificar, harás

El otro tropezamos con el siguiente artefacto:

a <- list(aa = 12, bb = 14)
is.null(a$a)
#[1] FALSE
a$a
#[1] 12

No es un bug de R, por que la documentación reza:

x$name is equivalent to x[[“name”, exact = FALSE]]

Y se pueden constrastar:

a[["a", exact = FALSE]]
a[["a", exact = TRUE]]

Comentarios:

• Odio muchísimo los bugs que no son bugs porque están documentados en el la nota ‡2.a.(c), párrafo §23.3 de la sección 14 de un manual oscuro.
• Odio mucho al os gilipollas que se complacen en mandarte a leer manuales.
• Odio mucho las violaciones del principio de mínima sorpresa.
• Soy consciente de que R es, fundamentalmente, una plataforma de análisis interactivo y no (o solo subsidiariamente) un lenguaje de programación.
• Soy consciente de que muchos de los defaults de R se decidieron antes de que se popularizasen los completadores de comandos.

Cuando tienes una serie temporal al uso (sin entrar a definir qué es eso), uno puede aplicar descomposiciones tmabién al uso, como stl, para extraer tendencia y estacionalidad, de la forma

como en esta entrada previa.

Lluvia.

La serie de la lluvia es otra cosa. Uno ve si llueve o no llueve (típicamente no). Lo que uno no ve es la probabilidad, que varía a lo largo del año, de que llueva. Pasa lo mismo con monedas (uno ve caras o cruces, no la probabilidad de cara), clientes que compran (uno ve si compra o no, no la probabilidad de compra), etc. Pero la probabilidad existe y en estimarla consiste frecuentemente el trabajo de algunos.

Me escriben pidiendo consejo sobre cómo leer datos contenidos en (una serie larga de) ficheros en formatos .dbf, .xlsx (con un formato extraño) y .pdf.

.dbf

No tengo ni curiosidad por averiguar de dónde proceden. Simplemente,

library(foreign)
res <-read.dbf("R0010.DBF")

funciona de maravilla.

.xlsx

Estos sí que sé de dónde vienen (y me guardo la opinión). El problema aquí no era leer directamente tablas contenidas en hojas sino ir extrayendo celdas y rangos de hojas. Así que:

Se ve que hay arqueólogos bayesianos. Un problema con el que se encuentran es que tropiezan con cacharros antiguos y quieren estimar su antigüedad.

Así que prueban distintos métodos (¿químicos?), cada uno de los cuales con su precisión, y acaban recopilando una serie de estimaciones y errores. Obviamente, tienen que combinarlas de alguna manera.

El modelo más simple es

$$ M_i \sim N(\mu, \sigma_i)$$

donde $latex \mu$ es la antigüedad (desconocida) del artefacto y los $latex \sigma_i$ son las varianzas distintas de los distintos métodos de medida, que arrojan las estimaciones $latex M_i$.