K-Medias

No hay nada tan corrosivo para la fe en el clústering que probar una y otra vez k-medias (por ejemplo) sobre los mismos datos y ver cómo los resultados cambian drásticamente de ejecución en ejecución.

Pero eso viene a ser, esencialmente, lo que hay detrás del consensus clústering (CC), una técnica que puede ser usada, entre otros fines, para determinar el número óptimo de grupos.

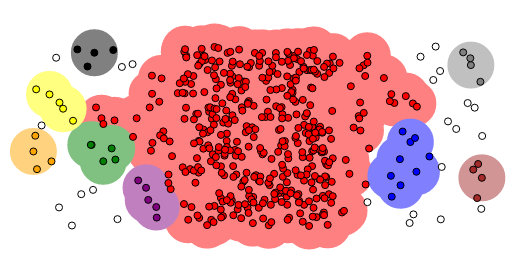
La idea fundamental de la cosa es que observaciones que merezcan ser agrupadas juntas lo serán muy frecuentemente aunque cambien ligeramente las condiciones iniciales (por ejemplo, se tome una submuestra de los datos o cambien las condiciones iniciales de k-medias, por ejemplo). Si uno altera esas condiciones iniciales repetidas veces puede contar la proporción de las veces que las observaciones i y j fueron emparejadas juntas y crear la correspondiente matriz (simétrica, para más señas) $latex C(i,j)$.

El otro día asistí a la enésima confusión sobre k-medias y k-vecinos. Que lo es, más en general, sobre el clústering contra modelos locales de la clase que sean, desde k-vecinos hasta el filtrado colaborativo. Veamos si esta comparación que traigo hoy a mis páginas contribuye a erradicar dicha confusión.

k-medias es como las elecciones. Hace poco tuvimos unas en España. Alguien decidió (aproximadamente) que k = 4 y nos pidió, a nosotros, punticos del espacio, identificar el centroide más próximo a nosotros para que lo votásemos. Pues eso, la misma frustración que muchos dizque sintieron teniendo que elegir entre partidos/centroides subjetivamente igual de alejados de los intereses de uno es la que sienten nuestros punticos cuando los procrusteamos para asociarlos al totum revolutum de los clientes estrella, etc.

En mi clase de aprendizaje no supervisado en el máster de ciencia de datos de la U-TAD mostré un vídeo en el que se ilustraba el funcionamiento del algoritmo de las k-medias.

Una alumna encontró un recurso mucho mejor.

Que trae, además, como bonus, una ilustración del funcionamiento de DBSCAN (véase también esto).

He encontrado una página que será, seguro, del gusto de mis lectores. Contiene animaciones en R tales desarrolladas con el paquete animation tales como ésta sobre la optimización por mínimos cuadrados o esta otra sobre k-medias.

¡A disfrutar!