Procesos Puntuales

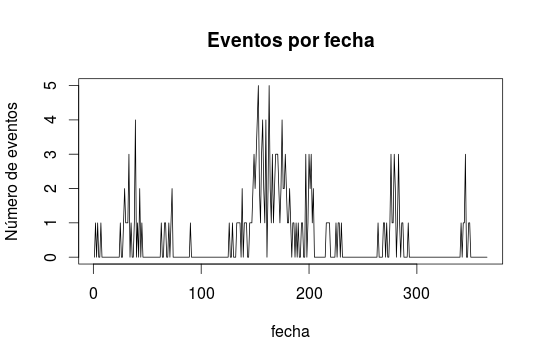
Fueron mis modelos favoritos un tiempo, cuando modelaba visitas y revisitas de usuarios a cierto malhadado portal. Si las visitas fuesen aleatorias (en cierto sentido), tendrían un aspecto no muy distinto del que se obtiene haciendo library(IHSEP) suppressWarnings(set.seed(exp(pi * complex(imaginary = 1)))) tms <- simPois(int = function(x) .1, cens = 1000) hist(tms, breaks = 100, main = "Proceso homogéneo de Poisson", xlab = "", ylab = "frecuencia") Es decir, o bien una distribución uniforme en el tiempo. Pero bien puede ocurrir que una visita incremente la probabilidad de otra inmediatamente después, por lo que las visitas tenderían a arracimarse en determinados momentos. Con el paquete [IHSEP](https://cran.r-project.org/package=IHSEP) de R pueden simularse (y ajustarse) este tipo de modelos. Por ejemplo, ...

Tuve que saltarme una diapositiva en el DataBeers de Madrid del pasado jueves. (A propósito, aquí están las 1+20 diapositivas.) La decimonona, de la que trata la entrada, viene a hablar de lo siguiente. Tenemos una base de datos con sujetos (ids) que hacen cosas en determinados momentos. No es inhabitual calcular la frecuencia de esos sujetos así: select id, count(*) as freq from mytabla where fecha between current_date - 7 and current_date group by id ; Esa variable se utiliza frecuentemente ya sea como descriptor de los sujetos o como alimento de otros modelos. ...

Lo que escribí hace un par de días sobre procesos puntuales, ahora me doy cuenta, podía haberse resuelto con nuestro viejo amigo glm. Ejecuto el código del otro día y obtengo (para un caso nuevo) mu alfa verosimilitud delta 1 0.4493158 0.50000000 340.6141 1 2 0.2675349 0.40457418 307.3939 2 3 0.1894562 0.28917407 293.4696 3 4 0.1495654 0.22237707 287.0784 4 5 0.1243791 0.18079703 281.3900 5 6 0.1142837 0.14913172 284.9227 6 7 0.1217504 0.12150745 288.5448 7 8 0.1214365 0.10424818 289.3282 8 9 0.1204605 0.09148817 290.9081 9 10 0.1315896 0.07857330 295.3935 10</code> que significa que el parámetro óptimo es delta = 5, mu = 0.124 y alfa = 0.18. Ahora hago cuantos.previos <- function(i, muestra, delta){ indices <- Filter(function(x) x < i & x > i - delta, 1:n) cuantos <- sum(muestra[indices]) } fit.glm <- function(delta){ prev <- sapply(1:length(muestra), cuantos.previos, muestra, delta) dat <- data.frame(muestra = muestra, prev = prev) res.glm <- glm(muestra ~ prev, data = dat, family = poisson(link = "identity")) c(delta, res.glm$coefficients, summary(res.glm)$aic) } res.glm <- sapply(1:10, fit.glm) res.glm <- as.data.frame(t(res.glm)) colnames(res.glm) <- c("delta", "mu", "alfa", "aic") y obtengo ...

Tengo una serie de datos que se parecen a lo que cierta gente llama procesos puntuales y que se parecen a los que se introducen (muuuuy prolijamente) aquí. Gráficamente, tienen este aspecto: Sobre un determinado periodo de tiempo (eje horizontal) suceden eventos y los cuento por fecha. Pero no suceden independientemente (como si generados por un proceso de Poisson) sino que tienden a agruparse: el que suceda un evento tiende a incrementar la probabilidad de que suceda otro poco después. El proceso, en una mala traducción, se autoexcita. ...