Tablas De Contingencia

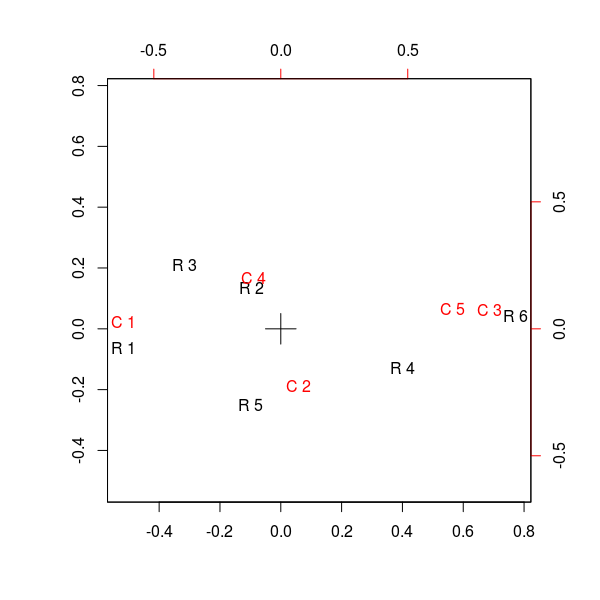
Con los datos pcts <- cbind( c(35.7, 19.6, 6.6, 16.6, 9.6), c(0.3, 0.2, 0.2, 0.3, 0.8), c(25.0, 14.9, 10.7, 32.7, 12.9), c(1.6, 8.0, 8.5, 6.5, 7.9), c(11.0, 18.7, 7.9, 12.7, 8.0), c(3.2, 21.5, 52.9, 16.7, 47.9) ) totales <- c(1102, 975, 596, 638, 174) tabla <- round(t(pcts * totales / 100)) y el concurso de library(MASS) biplot(corresp(tabla, nf = 2)) genero que a lo mejor no resulta demasiado interesante si no añado que las columnas se refieren a partidos políticos y las filas a cadenas en las que, según el CIS, sus votantes prefieren para seguir la actualidad política. Eso sabido, ¿cuál es cuál?

Hace unos días recibí una consulta de una vieja amiga lingüista. Ella trabaja en algo que creo que se llama cocolocación: el estudio de palabras que aparecen o que tienden a aparecer juntas en textos. Digamos que es algo así como una correlación o una regla de asociación. Los lingüistas están muy interesados en ese tipo de fenómenos. Tradicionalmente (cada gremio tiene su librillo) usan la información mutua. Pero, al final, lo que tienen es una tabla de contingencia: situaciones en que aparece una, la otra, ambas o ninguna de las palabras. ...

Abandonamos el otro día nuestra discusión sobre la feliz conjunción estadístico-algebraica que subyace a esa técnica conocida como análisis de correspondencias en el punto en que habíamos descompuesto la matriz $B$ de la forma $B = PDQ^\prime$, donde $P$ y $Q$ son matrices cuyas columnas son vectores ortonormales $p_i$ y $q_j$ y $D$ es una matriz diagonal (aunque no necesariamente cuadrada) cuyos elementos de la diagonal (en orden decreciente) son $\lambda_k$. ...

Tomemos una tabla de contingencia, p.e., library(MASS) a <- as.matrix(caith) # fair red medium dark black # blue 326 38 241 110 3 # light 688 116 584 188 4 # medium 343 84 909 412 26 # dark 98 48 403 681 85 que se refiere a los habitantes de una población de Escocia clasificados según el color de los ojos y el pelo. ¿Habrá una relación entre ambas variables? ...