De la varianza en muestras pequeñas (y el problema del hospital)
En un artículo que enlacé hace un tiempo se planteó el que después recibiría el nombre del problema del hospital:
En una ciudad hay dos hospitales. En el grande, hay, en promedio, 45 partos al día; en el pequeño, 15. La probabilidad de que un recién nacido sea niño o niña se supone igual al 50 %. ¿En qué hospital es más probable que en un día dado la proporción de niñas exceda el 60%?
En el artículo se menciona cómo en una muestra de 95 estudiantes universitarios, 21 se decantaron por el grande, 21 en el pequeño y 53 dijeron que la probabilidad es (aproximadamente) igual para ambos.
En realidad, si $latex X$ es el número de niñas nacidas en un hospital en el que ha habido n partos, entonces
$$ P( X / n > 0.6 ) = P( \frac{ X - n/2} {\sqrt{n}} ) > 0.1 \sqrt{n} ) \approx P( \Phi > 0.1 \sqrt{n} ) $$
donde $latex \Phi $ es una variable aleatoria N(0,1). Esta probabilidad puede calcularse en R escribiendo
1 - pnorm(0.1 * sqrt(15))
1 - pnorm(0.1 * sqrt(45))Efectivamente, uno de los errores en los que caemos al estimar probabilidades es que tendemos a ignorar que hay más variabilidad en grupos pequeños que en grupos grandes. Howard Wainer, en su artículo La ecuación más peligrosa, recoge otros casos de errores que se cometen por este mismo motivo.
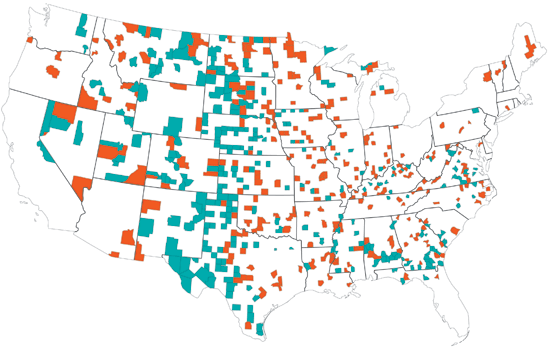
Y nos ayuda a entender gráficos como el que sigue. En el que aparecen pintados con distinto color los condados estadounidenses donde hay mayor y menor incidencia del cáncer de riñón:
Los que sepan algo sobre la geografía de ese país advertirán cómo ambos colores abundan más en zonas rurales, en los estados más despoblados. ¿Una misma causa (vivir en ese tipo de lugares), dos efectos opuestos? No, nada que ver con eso: el motivo es que cuando el denominador —la población— es pequeño, una ligera variación en el numerador —los casos de cáncer— pueden provocar cambios importantes en el cociente —la tasa de incidencia—. Lo que ese gráfico ilustra, en el fondo, no es una relación entre condicionantes geográficos y cierto tipo de cáncer sino cómo aumenta la varianza de la media de una serie de observaciones al disminuir su número.
El artículo recoge y cuestiona otras verdades, como la de que los alumnos de las escuelas pequeñas aventajan a los de las grandes, otra manifestación del mismo fenómeno.
¿Se le ocurrrirá a alguno de mis lectores algún ejemplo de este tipo de error en un contexto no estadounidense?
