Intervalos de credibilidad para la distribución beta
Tengo un parámetro, la p de una binomial, que supongo distribuido según una beta. Me da igual para el caso si la distribución a priori es o no informativa. Solo digo que la distribución a posteriori es otra beta con parámetros a y b.
Quiero construir un intervalo de credibilidad para p, es decir, encontrar un subintervalo de [0,1]
- dentro del cual la densidad de la beta sea mayor que fuera y que
- capture $latex 1-\alpha$ de la probabilidad total.
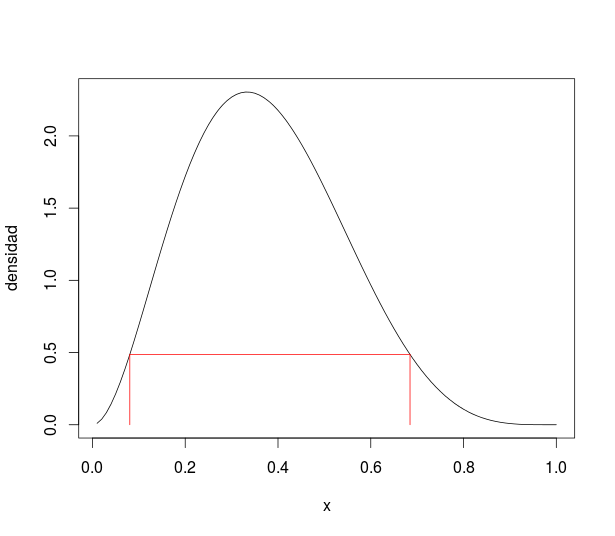
Gráficamente,
Y he aquí el código:
a <- 3
b <- 5
alfa <- 0.05
f <- function(x){
(dbeta(x[2], a, b) - dbeta(x[1], a, b))^2 +
(pbeta(x[2], a, b) - pbeta(x[1], a, b) -1 + alfa)^2
}
res <- optim(c(a/(a+b), a/(a+b)), f)
x <- 1:100 / 100
plot(x, dbeta(x, a, b), type = "l", ylab = "densidad")
lines(c(res$par[1], res$par[1]),
c(0, dbeta(res$par[1], a, b)), col = "red")
lines(c(res$par[2], res$par[2]),
c(0, dbeta(res$par[2], a, b)), col = "red")
lines(c(res$par[1], res$par[2]),
rep(dbeta(res$par[2], a, b), 2), col = "red")La función que se optimiza tiene como argumentos los puntos inicial y final del intervalo y penaliza:
- Que la densidad en dichos punto sea distinta.
- Que la suma de las probabilidades de las colas descartadas sea distinta de $latex \alpha$.
Una posible mejora en el código anterior sería pasarle a optim mejores puntos de partida: en lugar de la media de la distribución para ambos casos, la media más (y menos) dos veces la desviación estándar.