¿Son normales las alturas (de los individuos)?

Diríase que sí. La altura de un individuo está sujeta a multitud de factores que suman y restan. Está la genética (que es el resultado de la suma y resta del impacto de muchos genes individuales). Está la dieta, está… Diríase, insisto, que la altura es el promedio de muchos efectos pequeños y no demasiado dependientes entre ellos.

Y en efecto, (una vez descargados los microdatos de la Encuesta Nacional de Salud de 2011),

adultos <- readLines("MicrodatoAdultos.txt")

sexo <- substring(adultos, 14, 14)
sexo <- factor(sexo, labels = c("hombre", "mujer"))

altura <- as.numeric(substring(adultos, 430, 432))

alturas <- data.frame(sexo = sexo, altura = altura)
alturas <- alturas[alturas$altura < 900,]

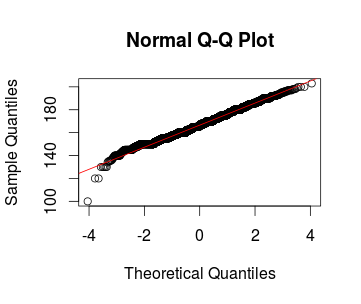
qqnorm(alturas$altura)
qqline(alturas$altura, distribution = qnorm, col = "red")

produce

donde, efectivamente, constatamos la normalidad de los datos con una pequeña salvedad: que hay individuos más bajos de lo esperado. Eso resta a nuestro argumento, pero no mucho. Diríase que son individuos afectados por un único efecto (¿genético?) poderoso que viola el principio de la suma de pequeños efectos independientes de más arriba.

¿Estamos satisfechos, pues, con lo de la normalidad de los datos? Si hacemos

library(ggplot2)
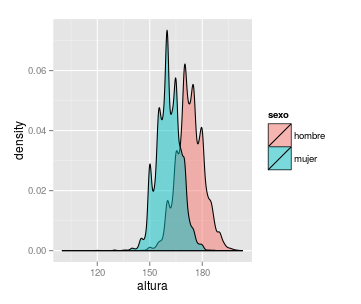
ggplot(alturas, aes(x = altura, fill = sexo)) +
    geom_density(alpha = 0.5)

obtenemos

y advertimos dos cosas. La primera es que algunos datos de altura están anotados a ojo: los picos que se aprecian corresponden a alturas redondeadas a la decena más próxima. Pero también que lo que creíamos una única distribución normal es, en realidad, la mezcla de dos: la de la alturas de los hombres y la de las mujeres.

Una mezcla de dos distribuciones con apariencia normal que resulta en otra distribución de apariencia también normal, de bimodalidad enmascarada, si se me permite.

La moraleja es que la altura se ve significativamente afectada por el efecto del (o la cascada de efectos determinada por el) sexo y que eso viola el principio de la suma de efectos independientes y pequeños.