GAM
Hoy he dado una charla en la Carlos III. En la comida me han preguntado, algo extrañados, por un ejemplo que había enseñado en el que ajustaba un modelo usando GAMs.
El motivo era que quienes preguntaban —que trabajan con ese tipo de modelos— encuentran muy difícil, se ve, convencer a otros usuarios de los métodos estadísticos (economistas, etc.) de adoptarlos. Yo he contestado que hace unos pocos días a unos primíparos que acababan de ajustar sus tres primeros lms con R les invité a probar GAMs con sus datos. ¿Por qué no?
La situación que teníamos planteada era parecida aunque un poco más complicada que esta:
irradiation <- read.table("http://rredc.nrel.gov/solar/old_data/nsrdb/1961-1990/hourly/1990/13994_90.txt",
header = F, skip = 1)
irradiation <- irradiation[,4:5]
names(irradiation) <- c("hour", "irradiation")
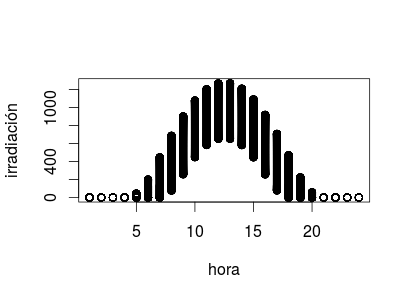
plot(irradiation$hour, irradiation$irradiation,
xlab = "hora", ylab = "irradiación")que produce
Obviamente, la irradiación solar (en San Luis, Misuri, durante el año 1990) depende grandemente de la hora del día.
Si uno prueba lo de siempre, lo que enseñan al principio, lo que parece que solo le está permitido a uno si no consigue cinturón negro en las artes del chamanismo estadístico, obtiene
mi.lm <- lm(irradiation ~ hour, data = irradiation)
summary(mi.lm)
# Call:
# lm(formula = irradiation ~ hour, data = irradiation)
#
# Residuals:
# Min 1Q Median 3Q Max
# -341.2 -336.9 -260.4 336.0 930.4
#
# Coefficients:
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) 335.4736 9.1814 36.538 <2e-16 ***
# hour 0.2408 0.6426 0.375 0.708
# ---
# Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#
# Residual standard error: 416.3 on 8758 degrees of freedom
# Multiple R-squared: 1.604e-05, Adjusted R-squared: -9.814e-05
# F-statistic: 0.1405 on 1 and 8758 DF, p-value: 0.7078
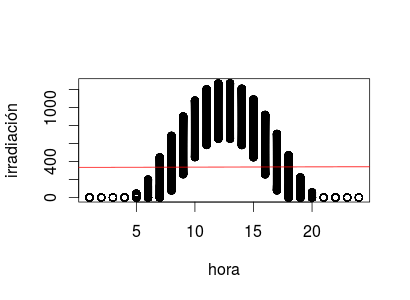
plot(irradiation$hour, irradiation$irradiation, xlab = "hora", ylab = "irradiación")
abline(mi.lm, col = "red")El gráfico obtenido, que muestra la predicción del modelo en rojo es
En resumen, la hora del día, aunque manifiestamente relacionada con la predicción, tiene un coeficiente nulo según los manuales al uso y quedaría fuera del estudio según los más de ellos. ¡Fijaos en ese p-valor tan tirrioso!
Contraintiutivo, ¿verdad?
¿Por qué no probar entonces con un modelo que recoja el efecto no lineal de la hora? En el menú tampoco hay tantas opciones y con suerte uno desemboca muy naturalmente en
library(mgcv)
mi.gam <- gam(irradiation ~ s(hour, bs = "cr"), data = irradiation)
summary(mi.gam)
# Family: gaussian
# Link function: identity
#
# Formula:
# irradiation ~ s(hour, bs = "cr")
#
# Parametric coefficients:
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) 338.484 1.647 205.5 <2e-16 ***
# ---
# Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#
# Approximate significance of smooth terms:
# edf Ref.df F p-value
# s(hour) 8.919 8.998 6122 <2e-16 ***
# ---
# Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#
# R-sq.(adj) = 0.863 Deviance explained = 86.3%
# GCV = 23799 Scale est. = 23772 n = 8760
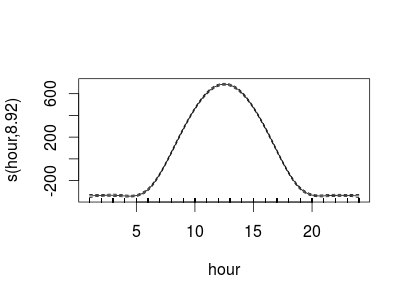
plot(mi.gam, xlab = "hora", ylab = "irradiación")que, ahora sí, produce
El resto de la discusión es poco relevante para los que tenemos prisa.
Y las notas:
- Sí, podemos en este caso usar la hora como variable categórica (¿pero qué si tenemos minutos, etc.?)
- Efectivamente, hay otras opciones en el menú. ¡Pero nos gusta la A de GAM!
- Quienes no descabalgan de los
(g)lmspuede que igual se dediquen a analizar datos demasiado tontos; o puede que igual no sepan lo que hacen… ¡pobrecicos! - Quienes se quejan de que los del punto anterior no descabalgan tal vez no hayan sabido dar con el conjunto de datos —les regalo el de hoy— para convencerlos.