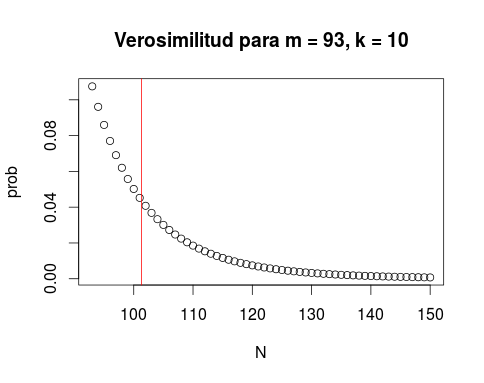
El problema de los tanques alemanes y de la máxima verosimilitud esquinada
El problema en cuestión, que se ve, surgió durante la II Guerra Mundial, es el siguiente: se capturan tanques del enemigo y se anotan los números de serie, supuestos sucesivos. ¿Cuál es la mejor estimación del número total de tanques fabricados por el enemigo?
Si se capturan k, la distribución del máximo número observado, m, en función del número no observado (nuestro parámetro) de tanques es
$$ f(N;m,k)=\frac{\binom{m-1}{k-1}}{\binom{N}{k}}$$
y como esta función es decreciente en $latex N$, la estimación por máxima verosimilitud es $latex \hat{N} = m$.
Obviamente, es una infraestimación. Y plantea un problema conocido: el del dilema entre plausible y probable. Tal vez, entre un conjunto de opciones plausibles, tal vez la más probable no lo es mucho más que el resto.
La Wikipedia propone dos soluciones distintas para este problema. La primera es la que me enseñaron en la universidad y que nunca acabé de comprender del todo:
- Se supone
Nconocido. - Se calcula el valor medio de
mpara dichoN. - Se estima el valor de
Ncomo aquél que daría una media igual al valor observado,m; es la que aparece, de hecho, en rojo en el gráfico anterior.
Podría llamarse método de estimación por máxima media.
La segunda solución que ofrece la Wikipedia es la bayesiana. Más bien, una de las bayesianas, la que tiene la particularidad de suponer que 3000 y 890613241273412 tanques son cifras igual de verosímiles a priori. Así puede convertir la verosimilitud graficada más arriba, convenientemente normalizada, en la distribución a posteriori del número de tanques.
El problema tiene su interés porque es uno de los pocos casos que conozco (o sobre los que haya pensado un poco) en el que, a diferencia de los más, el estimador por máxima verosimilitud está esquinado y parece más sensato recurrir a un estimador basado en una medida de centralidad para que los errores puedan serlo por arriba o por abajo.