¿Se puede explicar la predicción de un modelo de caja negra?

Imaginemos un banco que construye modelos para determinar si se concede o no un crédito. Este banco tiene varias opciones para crear el modelo. Sin embargo, en algunos países el regulador exige que el banco pueda explicar el motivo de la denegación de un crédito cuando un cliente lo solicite.

Esa restricción impediría potencialmente usar modelos de caja negra como el que construyo a continuación:

library(randomForest)

raw <- read.table("http://archive.ics.uci.edu/ml/machine-learning-databases/credit-screening/crx.data",
    sep = ",", na.strings = "?")

dat <- raw
dat$V14 <- dat$V6 <- NULL    # me da igual
dat <- na.omit(dat)          # ídem

modelo <- randomForest(V16 ~ ., data = dat)

Fijémonos en el sujeto 100, a quien se le deniega el crédito (suponiendo, ¡mal hecho!, que el punto de corte de la probabilidad para concederlo es el 50%), y la variable $V8$. Podemos ver cuál sería el score del cliente modificando esa variable entre su valor real y el máximo del rango dejando las demás tal cual:

n <- 20
tmp <- dat[100,]
tmp <- tmp[rep(1, n),]
tmp$V8 <- seq(tmp$V8[1], max(dat$V8), length.out = n)

tmp$pred <- predict(modelo, tmp, type = "prob")[,2]

plot(tmp$V8, tmp$pred, type = "l", ylab = "scoring")
points(tmp$V8[1], tmp$pred[1], col = "blue")
abline(h = 0.5, col = "red")

Eso produce

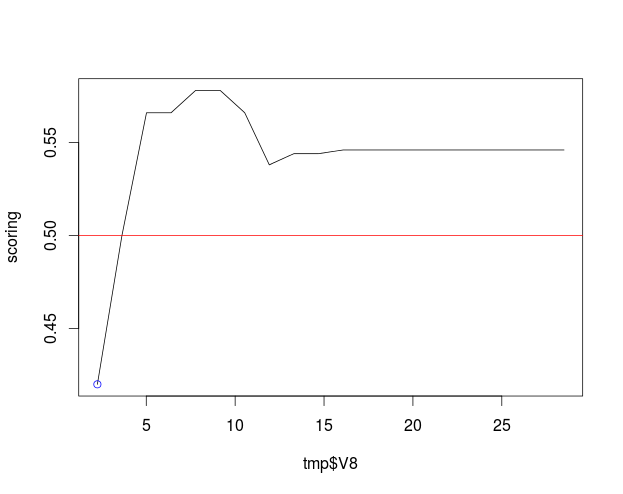
que permitiría explicarle a 100 cómo si su V8 fuese de alrededor de 4 en lugar de su mísero 2.25 habría podido acceder al crédito. Así con el resto de las variables relevantes.

(Nota: la curva anterior debería ser monótona. El hecho de que no lo sea podría deberse al tamaño ridículamente pequeño del conjunto de datos).

No creo que el regulador se diese por satisfecho con esto. Pero esa es otra de las guerras en las que, felizmente, no estoy.