Experimentos con "extremely small data": la media muestral de pocas betas

Aquí, contracorriente. Dejamos aparcado el big data y le damos a lo que nos da de comer. Entre otras cosas, este pequeño experimento con muy pequeños datos (¿tres?).

La aplicación es real. Y los datos pequeños porque son carísimos.

Se puede suponer que tienen distribución beta de parámetros desconocidos. Nos interesa la media muestral de unas pocas observaciones: dos, tres, cuatro,… En particular, qué distribución tiene.

Si fuesen muchos, podríamos aplicar el teorema central del límite (que funciona estupendamente incluso con valores no muy grandes). Pero la suma de pocas observaciones beta no tiene una distribución con nombre (que yo sepa). Pero podemos usar un viejo truco (parecido al de la aproximación de Welch para el número de grados de libertad de la prueba de Student cuando las varianzas son desiguales):

• Suponer que la distribución de la suma puede aproximarse por una beta.
• Estimar sus parámetros (por máxima verosimilitud en este caso).

Vamos a ello. Primero, generamos una muestra (tamaño 10000) de medias de tres muestras de la beta (con parámetros prefijados):

library(MASS)

reps <- 10000
n    <- 3

parms <- c(4, 49)

muestra <- function(n, reps, parms){
  tmp <- matrix(rbeta(n * reps, parms[1], parms[2]), n, reps)
  colMeans(tmp)
}

mi.muestra <- muestra(n, reps, parms)
hist(mi.muestra, breaks = 50, freq = F)

La pinta de la cosa es:

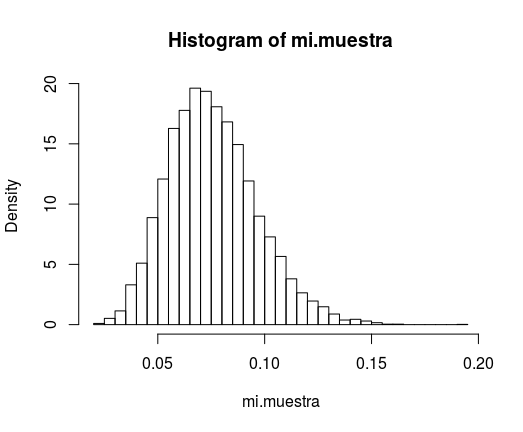
Y ahora,

res <- fitdistr(mi.muestra, "beta",
                start = list(shape1 = parms[1] * n,
                              shape2 = parms[2] * n))
curve(dbeta(x, res$estimate[1], res$estimate[2]),
      col = "blue", add = T)

produce

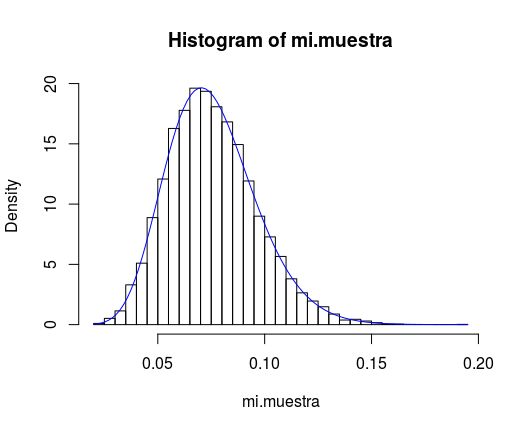
Pas mal!

Además, los parámetros resultantes están próximos a n veces los originales. Algo que no es enteramente evindente: la varianza de la media muestral debería ser la original dividida por n; pero la fórmula de la varianza de la distribución beta

$$ \frac{\alpha \beta}{(\alpha + \beta)^2 (1 + \alpha + \beta)}$$

no es homogénea en sus parámetros (pero casi).