Sobre el problema de las martingalas: ¿cuántos sabíais la respuesta?

Estadística

Pues no se sabe bien. Además, habrá quién pudiéndola haber averiguado, prefirió dejarse llevar por la intuición y errar. Pero volvamos a los hechos. Dado

la pregunta urgente es: ¿cuántos podrían haber conocido la respuesta? Suponiendo que el conocimiento de la respuesta es algo binarizable (¿lo es?), la distribución del número de respuestas correctas sería $latex pN + X$, donde $latex N$ es el número total de respuestas, $latex p$ es la proporción de quienes sabe la respuesta y $latex X \sim B(N - pN, 1/3)$, suponiendo siempre que $latex pN$ es entero.

En realidad, el número de aciertos, así considerado, es una mezcla de dos binomiales, una con probabilidad de acierto del 100% y otra del 33.3%. Así que

library(rstan)

N <- 782
correctas <- round(N * 0.38)


standat <- list(N = N, correctas = correctas)

stanmodelcode <- '
data {
  int N;
  int correctas;
}

parameters {
  real<lower = 0, upper = 1> p;
}

model {
  real prob;
  real accum;

  // priori
  p ~ beta(1, 1);

  accum = 0;

  for(i in 0:correctas){
    prob  =  binomial_lpmf(i | N, p) +
      binomial_lpmf((correctas - i) | (N - i), 0.3333);
    accum = accum + exp(prob);
  }

  target += log(accum);
}
'
fit <- stan(model_code = stanmodelcode,
            data = standat,
            #init = rep(list(list(p = 0)), 4),
            iter=12000, warmup=2000,
            chains=2, thin=10)

res <- as.data.frame(fit)
hist(res$p, freq = FALSE, col = "gray",
     main = "distribución de p",
     xlab = "", ylab = "")

para obtener el vergonzante

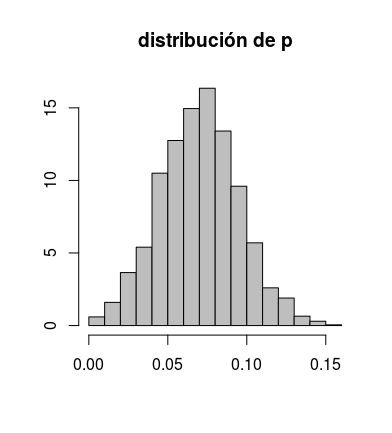
De todos modos, debo añadir que durante las primeras horas de la encuesta, el porcentaje de aciertos llegó a estar en el entorno del 50%. Después fue retuiteado y el porcentaje descendió lastimosamente. Quiere eso decir cosas muy buenas de quienes me siguen en Twitter. Al menos, en términos relativos.