vecpart: modelización de moderadores con árboles
En un GLM (aún más generalizado que la G de las siglas) puede haber coeficientes moderados. Usando una terminología muy ad hoc, en el modelo pueden entrar predictores y moderadores. Lo cual quiere decir que la parte lineal puede ser de la forma
$$\sum_i X_i \beta_i(Z_i),$$
donde las $latex X_i$ son los predictores propiamente dichos y las variables $latex Z_i$ son moderadoras, es decir, que modifican el efecto de los predictores a través de una función arbitraria $latex \beta_i$.
Un ejemplo: el efecto del colesterol puede depender de la edad del paciente.
Este tipo de efectos se pueden modelar vía interacciones. O con splines. O con kernels. (Más abajo hay una referencia con referencias).
Pero también, ¿por qué no?, con árboles. Eso hace el paquete vcrpart de R. Con él, uno puede decirle al modelo: tal variable depende de estas otras y créame el típico árbol (al estilo de ctree o mob en party) que aproxime la relación funcional. Lo que permite estudiar muy concretamente el efecto de los moderadores en el impacto de una variable, etc.
Como abrebocas,
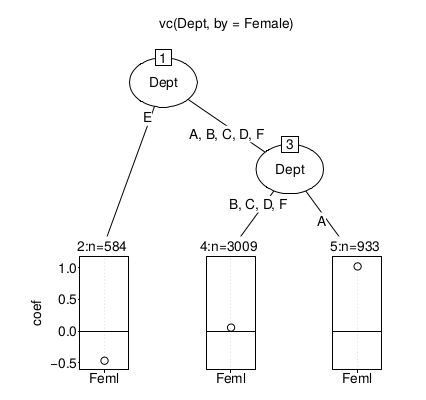
que describe la manera en que el departamento modera el coeficiente del sexo en el famoso conjunto de datos de las admisiones de Berkeley. (Sí, ya sé que lo mismo se puede hacer con interacciones de toda la vida pero… ¿no es cómodo que el algoritmo ya encuentre no significativamente distintos los coeficientes relativos a los departamentos B, C, D y F?).
Y la cosa completa, junto con las referencias arriba prometidas, en Coefficient-Wise Tree-Based Varying Coefficient Regression with vcrpart.
Nota: ¿no es todo esto tremendamente parecido a los modelos jerárquicos?
