Simulación de procesos de Poisson no homogéneos y autoexcitados

Consultoría, Estadística, R

Fueron mis modelos favoritos un tiempo, cuando modelaba visitas y revisitas de usuarios a cierto malhadado portal.

Si las visitas fuesen aleatorias (en cierto sentido), tendrían un aspecto no muy distinto del que se obtiene haciendo

library(IHSEP)

suppressWarnings(set.seed(exp(pi * complex(imaginary = 1))))

tms <- simPois(int = function(x) .1, cens = 1000)
hist(tms, breaks = 100, main = "Proceso homogéneo de Poisson",
      xlab = "", ylab = "frecuencia")

Es decir,

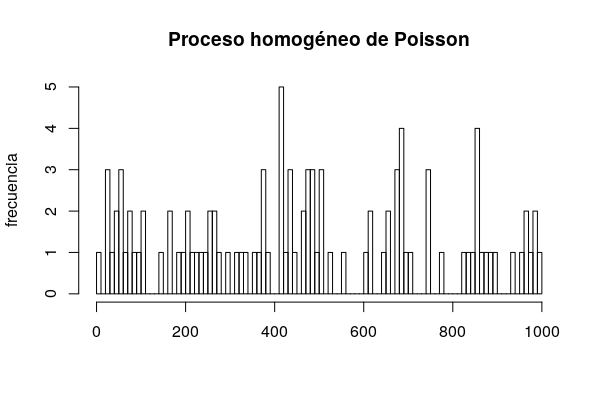
o bien una distribución uniforme en el tiempo. Pero bien puede ocurrir que una visita incremente la probabilidad de otra inmediatamente después, por lo que las visitas tenderían a arracimarse en determinados momentos. Con el paquete [IHSEP](https://cran.r-project.org/package=IHSEP) de R pueden simularse (y ajustarse) este tipo de modelos. Por ejemplo,

res <- simHawkes1(nu = function(x) .1,
    g = function(x) .5 * exp(-x), cens =1000)
hist(unlist(res), breaks = 100,
main = "Proceso autoexcitado",
      xlab = "", ylab = "frecuencia")

proporciona

que es más realista. La magia es obra de la función g, que incrementa la probabilidad de nuevos eventos después de que ocurra alguno, aunque la estela que dejan decae exponencialmente (por construcción).

Notas:

  • Los procesos anteriores tienen una base homogénea (la función de intensidad base se ha definido igual a .1), pero podría utilizarse una función de t arbitraria que los convertiría en procesos no homogéneos.
  • El paquete también proporciona mecanismos para estimar tanto la función base como la de autoexcitación. Que no sé qué tal funcionarán. Y si lo harán en tiempo y forma.