Imaginemos que queremos categorizar textos (i.e., poder decir algo así como: el texto 1434 trata de biología). Una manera de afrontar el problema, no la única, es contar palabras (o más en general, términos: piénsese en bigramas, trigramas, etc.).
Qué es
Por fijar ideas, pensemos en textos sobre economía (sí, porque voy a referirme a parte del análisis de los textos del blog nadaesgratis.es al que ya me referí aquí).
En total, en casi 33 MB de texto hay muchos términos (estrictamente, unigramas): en total, 81618 lemas (de acuerdo con la definición de Spacy de lema). Tiene sentido filtrar los términos para seleccionar solo aquellos más relevantes para clasificar los textos. Así, por ejemplo:
- Puede pensarse que términos como para o y no van a ser muy útiles para clasificar textos dado que se encuentran por doquier en todos. Pueden eliminarse de oficio y, de hecho, cualquier software de NLP incluye listas de stopwords (que incluyen esos términos junto con algunas docenas más) genéricas.
- En el extremo contrario están palabras como sífilis, que aparecen muy pocas veces (de hecho, solo en una ocasión en el texto de referencia) y que mal van a poder ser indicativo de nada (salvo que se agrupen por hiperónimos, algo que no sé si el software al uso es capaz de hacer).
- En este caso concreto, palabras como economía es posible que tampoco resulten útiles: cabe esperar que aparezcan también en la mayoría de los textos. Son, en cierto modo, stopwords locales.
- Pero otras como industrial, FMI, causalidad, etc. pudieran parecer útiles para la labor que nos proponemos desarrollar.
¿Qué propiedades cumplen, por tanto, los términos útiles?
- Tienen que aparecer con cierta frecuencia en los textos.
- Pero solo deberían aparecer en cierto númoero de ellos, no en todos.
Lo cual conduce de manera natural al TF-IDF. El TF-IDF es una familia de indicadores que tiene la siguiente propiedad:
- Es creciente con la frecuencia de cada término.
- Es decreciente con el número de documentos en el que aparece.
Digo que es una familia de indicadores porque hay varias formas de operacionalizarlo, ninguna de ellas es universalmente útil y uno debería usar la versión que más y mejor encajase en su proyecto.
El siguiente gráfico muestra la TF (frecuencia de los lemas, abscisas) y cierta versión del IDF (frecuencia inversa en documentos, ordenadas) de los 300 términos más frecuentes (una vez eliminados stopwords globales y locales) en los textos de Nadaesgratis.
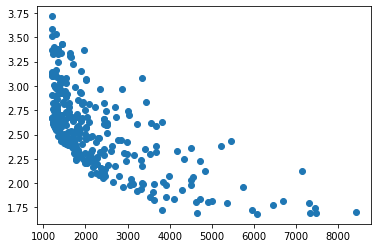
Globalmente, se observa lo que se espera: una relación inversa entre el TF y el IDF. Sin embargo, hay términos como mujer (TF ~ 3500, IDF ~ 3) o empresa (TF ~ 7000, IDF ~ 2) que están fuera (y en el lado bueno) de la hipérbola.
Dónde usarlo
Obviamente, puede ser usado para seleccionar términos relevantes.
Otro uso del que hablaré pronto tiene que ver con el uso de embeddings para capturar el asunto de cada entrada. Un embedding es una aplicación que asigna a cada término un vector en un espacio de dimensión alta (¿$R^{256}$?). Un embedding bien hecho promete recoger el sentido del término (es decir, que términos similares o relacionados tienen embeddings próximos).
Uno puede —y ciertos módulos de NLP lo hacen así— tratar de recoger el sentido de un documento promediando los embeddings de cada uno de los términos que lo componen. Pero uno puede hacerlo mejor (supongo: todo esto es más alquimia que ciencia propiamente dicha) promediando solo los términos más relevantes y modulando además los pesos con el IDF (de manera que términos con IDF alto pesen más en el vector final).
Dónde no usarlo
Pero he visto también usos raros del TF-IDF. Imaginemos que uno quiere crear un modelo que distinga textos. Para eso, selecciona los términos $t$ de interés y para cada documento $d$ crea una matriz cuya entrada $(d, t)$ es un número que representa la importancia de $t$ en $d$. Puede ser la frecuencia bruta, la frecuencia relativa, el logaritmo de la frecuencia (más uno), etc.
Pero algunos incluyen también el IDF. Es decir, aplican —típicamente, multiplicando— el IDF a cada término. En plata, multiplican (o escalan) cada columna de la matriz por un valor. Lo cual no tiene ningún sentido en absoluto si el modelo que uno acaba aplicando es, como tantas veces, lineal (tal cual o generalizado vía logísticas o, aún más en general, RRNN densas).
Pero, ¡ah!, hay situaciones donde usar el IDF de esta manera estúpida puede funcionar subrepticiamente. Describo un caso:
- No sabes lo que estás haciendo: básicamente, copias código de otro.
- Usas Python + Scikit-Learn.
- Empleas un modelo logístico (aunque lo que comento también podría aplicarse a otro tipo de modelos).
En tal caso, es fácil que usar IDF mejore el modelo. El motivo es que:
- El modelo logístico de Scikit-Learn no es la regresión logística sino su versión ridge (por defecto, aunque puede especificarse lasso o el GLM tradicional).
- Ridge penaliza más las columnas con valores promedio bajos.
- Luego usar el IDF en este contexto, subrepticiamente, penaliza el impacto de los términos con un IDF pequeño.
Y sí, este es un caso más en el que los tontos tienen suerte.