Una regresión de Poisson casi trivial con numpyro

Estadística

El otro día hubo, parece, cierto interés por modelar la siguiente serie histórica de datos:

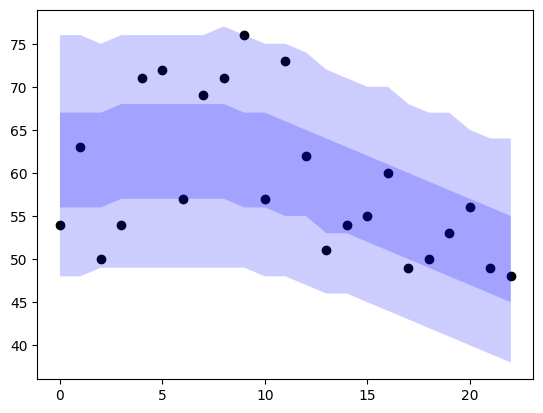
Notas al respecto:

  1. El eje horizontal representa años, pero da igual cuáles.
  2. El eje vertical son números naturales, conteos de cosas, cuya naturaleza es poco relevante aquí, más allá de que se trata de eventos independientes.
  3. Se especulaba con un posible cambio de tendencia debido a una intervención ocurrida en alguno de los años centrales de la serie.

Lo que se ve es el resultado del ajuste de un modelo de Poisson casi trivial. Es casi trivial porque utiliza el tipo más simple de splines para modelar una tendencia quebrada en un punto desconocido, uno de los parámetros del modelo.

Las bandas representan intervalos de confianza al 50% y 90% respectivamente. Que nos dan a entender que el ajuste no es demasiado allá dado que:

  1. En el primer bloque de la serie parece haber más dispersión de la esperada.
  2. Y menos, en el segundo.
  3. Es raro que ningún punto quede fuera de las bandas.

Por referencia, el modelo descrito más arriba es:

def model02(t, datos):
  knot = numpyro.sample("knot", dist.Normal(len(t)/2, len(t)/4))

  a0 = numpyro.sample("a0", dist.Normal(60, 5))
  b0 = numpyro.sample("b0", dist.Normal( 0, 1))

  b1 = numpyro.sample("b1", dist.Normal(0, 1))

  λ = a0 + t * b0 + jnp.where(t > knot, (t - knot) * b1, 0)

  with numpyro.plate("data", len(t)):
    numpyro.sample("obs", dist.Poisson(λ), obs=datos)

Y la distribución a posteriori del nudo en el cual se produce el cambio de tendencia postulado es

El código completo puede verse aquí.