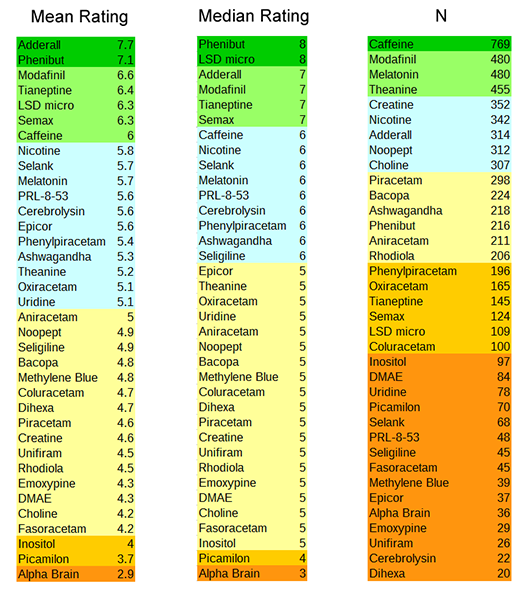
Regresión tradicional vs multinivel
Ayer se leía en Twitter que
"La regresión multinivel debería ser la forma predeterminada de hacer regresión"
— Jose Luis Cañadas (@joscani) April 11, 2020
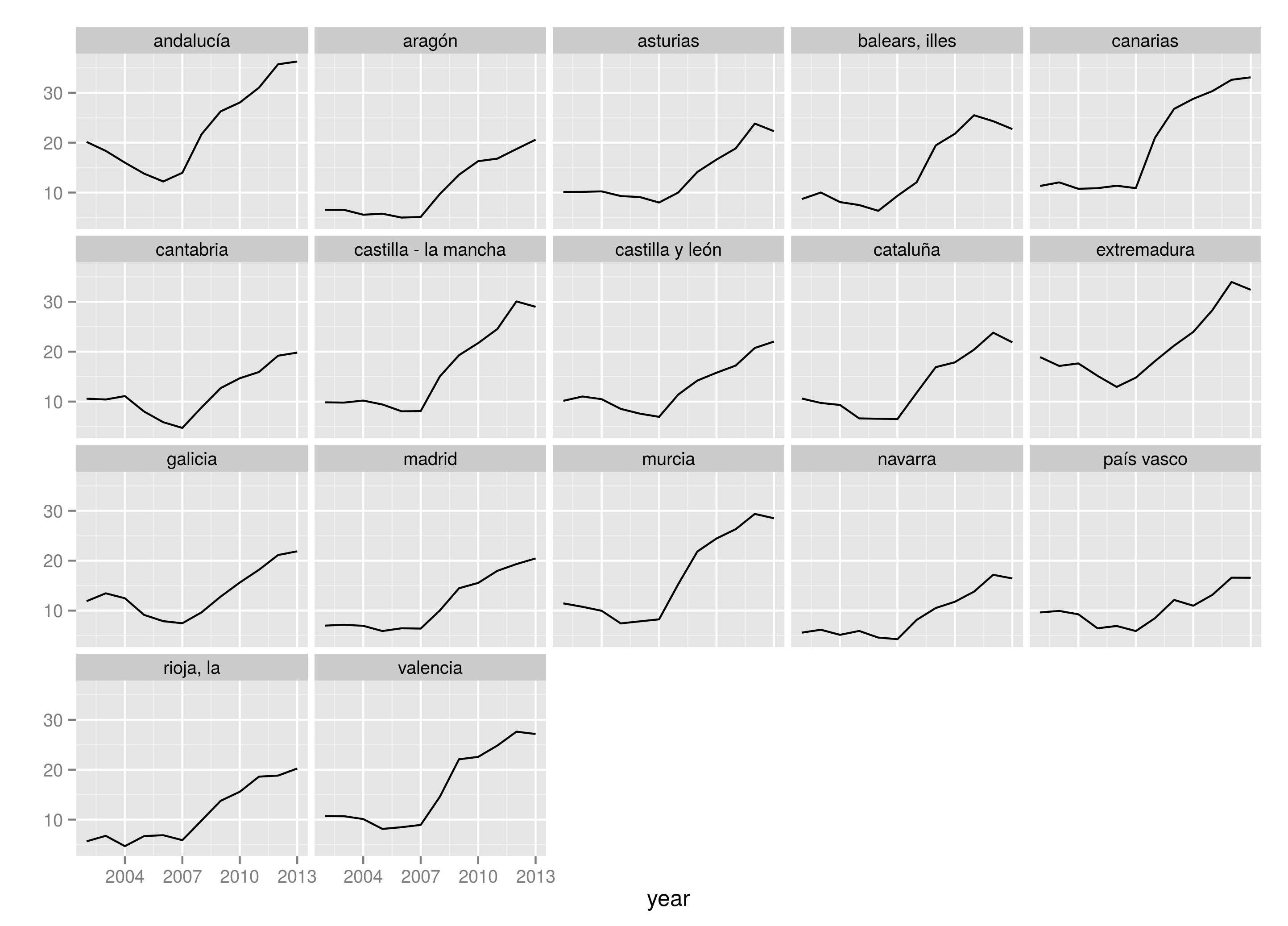
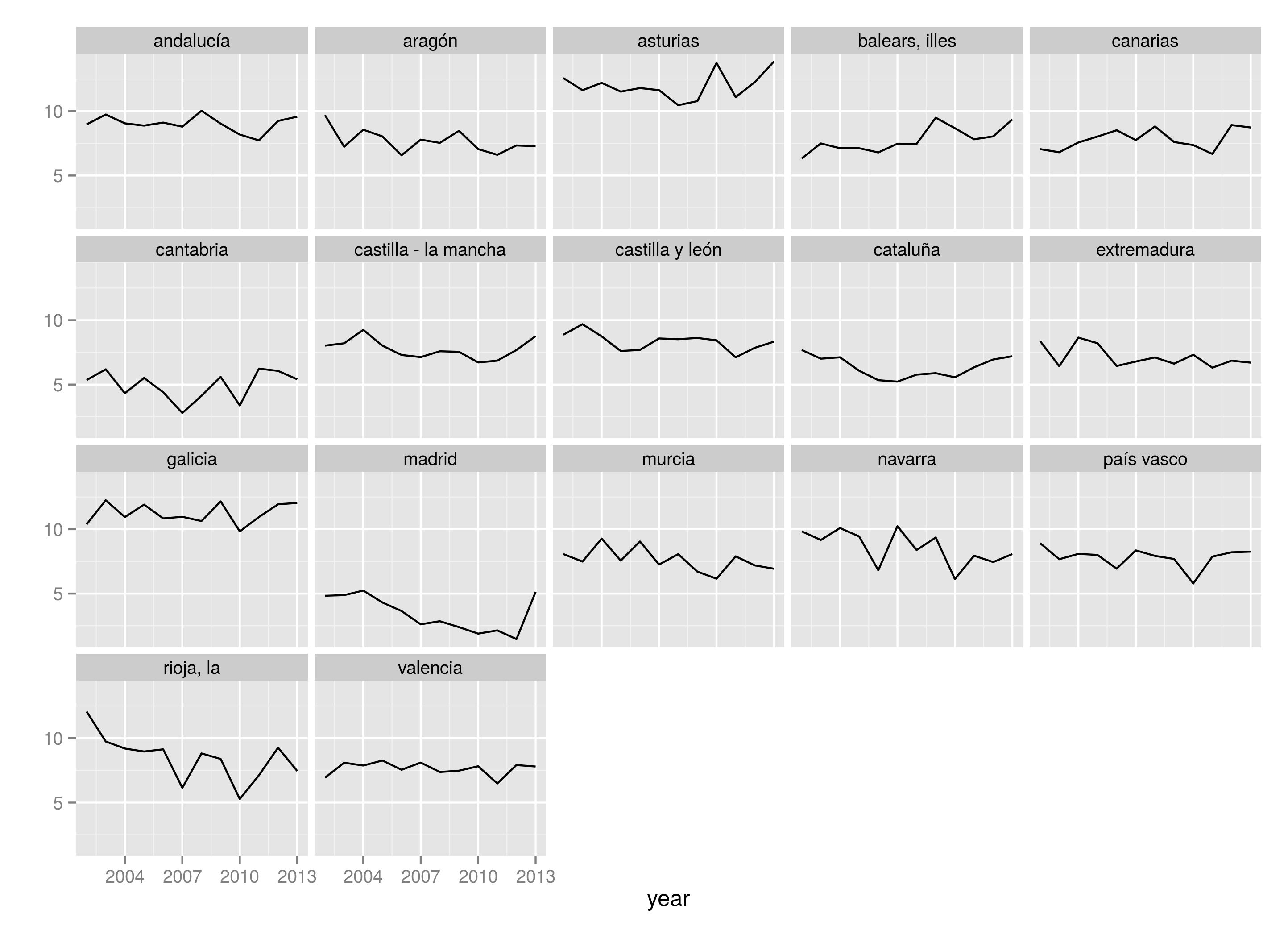
Cabe preguntarse qué pasa si se analizan los mismos datos usando ambas técnicas. Obviamente, hay muchos tipos de datos y supongo que los resultados variarán según qué variante se utilice. Aquí voy a centrarme en unos donde hay medidas repetidas de un factor aleatorio. También voy a situarme en un contexto académico, en el que interesan más las estimaciones de los efectos fijos, que en uno más próximo a mi mundo, la consultoría, donde son más relevantes las estimaciones regularizadas de los efectos aleatorios.