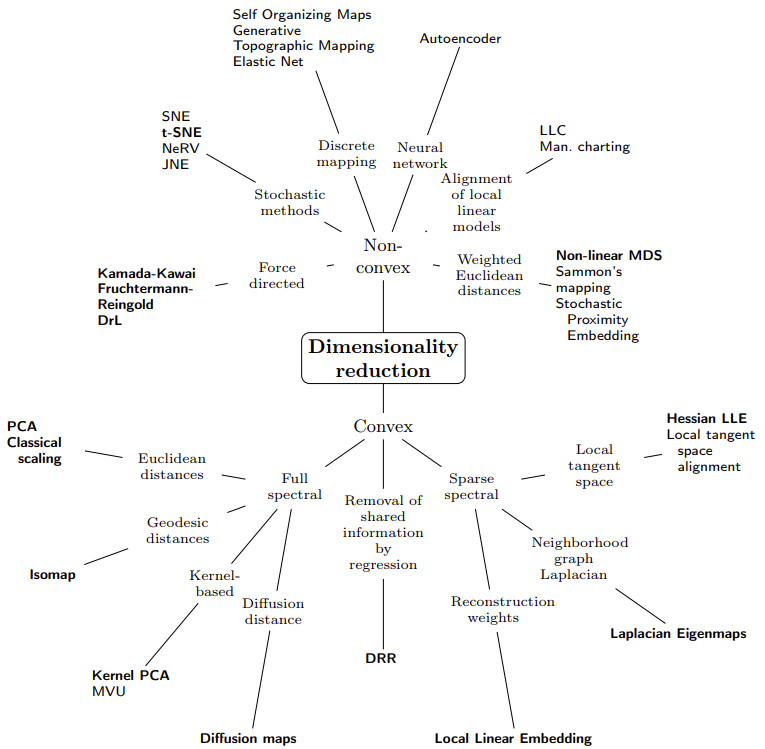
Autoencoders: una serie de lecciones aprendidas
Estos días pasados he tenido que usar autoencoders como mecanismos para reducir la dimensión de una serie de conjuntos de datos. El principal problema al que me he enfrentado —cómo no— ha sido el de diseñar una arquitectura adecuada para el problema en cuestión. El principal motivo es que la práctica totalidad de los tutoriales, ejemplos, etc. disponibles por ahí tienen como aplicación principal el tratamiento de imágenes y en mi caso no.