La escala natural de la varianza

Supongo que lo que voy a contar hoy es conocido de muchos de mis lectores. Desafortunadamente, uno tropieza con más frecuencia de lo deseable con quienes no lo son. (Eso sí, uno de los mayores placeres de esta vida es coincidir con alguien que te reconoce y te dice: “¿tú tienes un blog que se llama datanalytics, ¿verdad?”; pero esa es otra historia).

Al grano.

Supongamos que tenemos un sistema con sensores que miden la temperatura (5) y la presión (2) en diversos puntos. Los dejamos recoger datos durante 100 periodos y obtenemos

set.seed(1234)

n <- 100

n.temp <- 5
n.pres <- 2

temp.global <- rnorm(n)
pres.global <- rnorm(n)

temp <- 0.2 * matrix(rnorm(n*n.temp), n, n.temp) +
    temp.global
pres <- 0.2 * matrix(rnorm(n*n.pres), n, n.pres) +
    pres.global

dat <- cbind(temp, pres)

dim(dat)
# [1] 100   7

head(dat)

# [,1]       [,2]       [,3]        [,4]       [,5]        [,6]        [,7]
# [1,] -1.1100204 -1.3230571 -1.4524288 -1.01010976 -1.1443700  0.50550395  0.20973698
# [2,]  0.4167830  0.0867735  0.2846598  0.03248167  0.3999239 -0.18963434 -0.75224859
# [3,]  1.1215440  1.0485555  1.0001626  1.22638642  0.7462245  0.02419526  0.05614927
# [4,] -2.2055510 -2.1437361 -2.5255706 -2.36754170 -2.1887580 -0.74875834 -0.14028564
# [5,]  0.4914609  0.4338500  0.5126130  0.78564627  0.4315097 -0.89811930 -0.84590060
# [6,]  0.6581484  0.3762502  0.5367448  0.45736696  0.4698048  0.05754662  0.32243670

Las primeras cinco columnas de esta tabla de datos simulados recogen la temperatura global del sistema más una señal propia de cada sensor (según su ubicación). Las dos últimas, la presión con la misma salvedad.

Ahora llega un señor importante, de los de corbata, uno de esos devoradores de articulillos del subgénero del márqueting ficción, y nos pide que hagamos big data.

Y a nosotros se nos ocurre reducir la dimensionalidad del problema usando componentes principales (PCA) así:

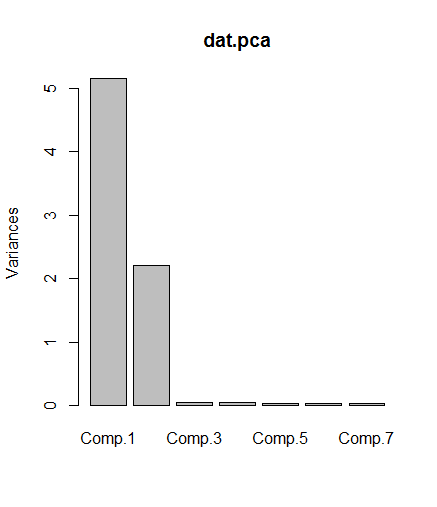
dat.pca <- princomp(dat)

Las dos primeras componentes principales tienen casi toda la varianza (como cabía esperar en nuestros datos artificiales):

screeplot(dat.pca)

Como puede verse haciendo

loadings(dat.pca)

# Loadings:
#   Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6 Comp.7
# [1,] -0.449               -0.247  0.804 -0.157 -0.245
# [2,] -0.456         0.418  0.394        -0.107  0.665
# [3,] -0.435        -0.825  0.111 -0.185  0.197  0.210
# [4,] -0.453         0.362 -0.229 -0.231  0.701 -0.258
# [5,] -0.443                      -0.486 -0.639 -0.389
# [6,]        -0.721        -0.592 -0.111 -0.106  0.324
# [7,]        -0.692         0.606         0.117 -0.360

la primera componente es una combinación lineal de (esencialmente, ¡no exclusivamente¡) las primeras cinco columnas (relacionadas con la temperatura) y la segunda, de las dos restantes (relacionadas con la presión).

Y todo esto ha sido el preámbulo de la pregunta que justifica la entrada de hoy: ¿qué tiene de superimportante la primera componente con respecto a la segunda?

En los libros se nos enseña que las componentes principales tienen importancia decreciente. La primera es la más guay, etc. Las últimas pueden desdeñarse. También se nos enseña que es recomendable estandarizar las variables para evitar, precisamente, que alguna de ellas domine al resto y pese demasiado en la primera componente principal (o que se identifique con ella en casos extremos).

Pero este es un caso que la literatura —al menos, la literatura que leen algunos a quienes podría señalar con el dedo— no plantea.

En este caso artificial, el peso de la primera componente no tiene causas intrínsecas. Se debe, simplemente, a que hay cinco sensores que miden la temperatura y solo dos que miden la presión. Si hubiese tres y tres —lo dejo planteado como ejercicio— las dos primeras componentes principales serían equivalentes.

Esto puede ser y no ser grave. De eso hablaré en los próximos días. Depende de qué se quiera hacer después con esas componentes.

Pero sí quiero dejar clara una cosa: en situaciones reales, en bases de datos grandes, con muchas columnas, la importancia relativa de las componentes principales puede decir tanto sobre la estructura matemática de los datos como, quizás, de algo mucho menos enjundioso: el número de variables que en la base de datos recogen cada uno de los, si se me permite, factores subyacentes (es decir, los equivalentes a la temperatura y la presión en nuestro ejemplo).

Y bueno, para terminar, un poco de erudición para quien quiera ahondar más en el asunto: MFA.