Causalidad a la Pearl y el operador do

Un tipo me pasó el librito de Pearl, Causality, y se ha pasado varios días dando la vara con que si me había leído ya el epígrafe. Pues sí, lo he leído este finde. Y no solo lo he leído sino que voy a escribir sobre ello.

Había tratado de leer cosas de Pearl en el pasado. Pero las encontraba demasiado llenas de letras difíciles de comprender si no se entendían bien las fórmulas. Que, a su vez, eran difíciles de comprender sin tener una idea clara de qué indicaban los diagramas adjuntos. Para cuya comprensión había que hacerse bien con el texto. Vamos, que nunca había sacado nada en claro. Aunque, confieso, la coyuntura en la que suelo leer ese tipo de cosas (metros, trenes, autobuses) tampoco me ayuda.

No obstante, me siento reivindicado: en el epígrafe arriba mencionado, Pearl demuestra saber también escribir para seres humanos.

Por si no estaba claro, el libro entero, la obra de Pearl entera, el mismo Pearl entero, trata sobre causalidad, sobre cuándo y cómo podemos decir que A es la causa de B.

La ciencia trata de esas cosas, a menudo. A veces no. A veces la ciencia se conforma en saber dónde caerá la bala sin importarle cuál es la naturaleza de la fuerza de la gravedad. Los higienistas descubrieron eso que lavarse las manos era conveniente antes incluso de que se conociesen los gérmenes. Etc. Hay muchas historias al respecto.

Además, el lenguaje (tradicional) de la ciencia no entiende de causalidad. Por ejemplo, Pearl se fija en la fórmula F = ma. Desde chavales nos enseñaron que la fuerza _causa _una aceleración (que depende de la masa). Pero aunque escribamos a = F/m, no caeremos en el error de decir que la aceleración causa una fuerza. Las ecuaciones pueden invertirse, pero las relaciones causales no.

De ahí que Pearl se haya esforzado en, primero, crear un lenguaje basado en símbolos, redes causales, que representan hipotéticas relaciones causales.

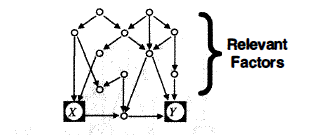
Por ejemplo, la temperatura podría afectar la resistencia de una fibra. Podría plantearse un diagrama simple con una flecha desde la temperatura a la resistencia. Y un ingeniero podría plantear un test para validar si, en efecto, es así. Los ingenieros, de hecho, pueden hacer experimentos en el que varíe únicamente un parámetro y poder así determinar el efecto de dicha intervención (aislada del resto de factores) en el objeto de interés.

Pero la ingeniería es una rareza. En otras disciplinas (¡yo que pensaba que había hablado ya de relojes, de gatos y de Madagascar en mi blog!) no es posible realizar tal tipo de experimentos (salvo que seas un Mengele en Auschwitz o un consultor de Podemos en Venezuela). En otras disciplinas no se dispone sino de estudios observacionales, no controlados.

La pregunta es: ¿es posible obtener resultados similares a los de los ingenieros utilizando únicamente resultados observacionales? La respuesta, según Pearl, es positiva. Para eso introduce un operador, do, que simula intervenciones junto con una serie de reglas probabilísticas. do(x) en una red probabilística es el efecto en cascada que tendría sobre los nodos subsecuentes una intervención hipotética que fijase el valor de x.

Por ejemplo, ¿qué pasaría con la tasa de paro si bajásemos los impuestos? Sustituiríamos IRPF por do(IRPF) en nuestra red probabilística y operaríamos sobre ella hasta eliminar, de ser posible, nuestro condicionante hipotético.

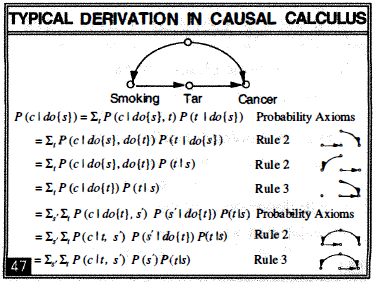
En el gráfico anterior hay un ejemplo. En una red causal, se introduce una intervención, do(s), y se opera con las reglas de la probabilidad y del operador hasta eliminarlo. Y eliminarlo significa que es posible deducir (o, al menos, testar) una relación de causalidad sin realizar un experimento al uso, simplemente utilizando resultados observacionales.

En fin, que os invito a leer el epígrafe en cuestión.

No obstante, dos observaciones de mi cosecha:

• Parece que Pearl es el enésimo ingeniero barra físico barra loquesea que se empeña matematizar lo muy difícilmente matematizable y estudiar fenómenos biológicos y sociales more geometrico. ¡Sea bienvenido al club!
• El ejemplito que desarrolla Pearl en el epígrafe me recuerda a cuando me enseñaban a integrar por partes. Uno llegaba a casa del colegio pensando que no iba a haber función que se le resistiera. Pero jamás le contaban que había que perder la esperanza: salvo unas cuantas funcioncitas bastante excepcionales, las de la hoja de problemas y pocas más, prácticamente ninguna tiene integral indefinida cerrada. Me da la sensación de que el álgebra de Pearl resolverá estupendamente siete ejemplos imprácticos y no tendrá apenas qué decir en el resto de los casos.