Respuestas distintas, ¿a la misma pregunta?

Hará ya un par de años, un señor muy importante divulgaba en su bitácora los resultados de un estudio relativo a la educación en España que acababa de publicar. Dedicaba una pequeña parte de la entrada a cuestiones metodológicas y el resto a cuestiones normativas: dado que he encontrado esto y aquello con un p-valor de tal, no otro remedio queda que aplicar todas estas medidas que aquí enumero, era el resumen de todo.

Venía yo de construir unos modelos similares y le pedí los datos. Quería ver si los p-valores se mantenían de pie o se daban la vuelta al proponer modelos alternativos aunque igualmente razonables. Se negó en redondo y ahí acabó la historia.

Estos días, muchos navegadores (incluido, ahora, el tuyo) han mostrado la imagen

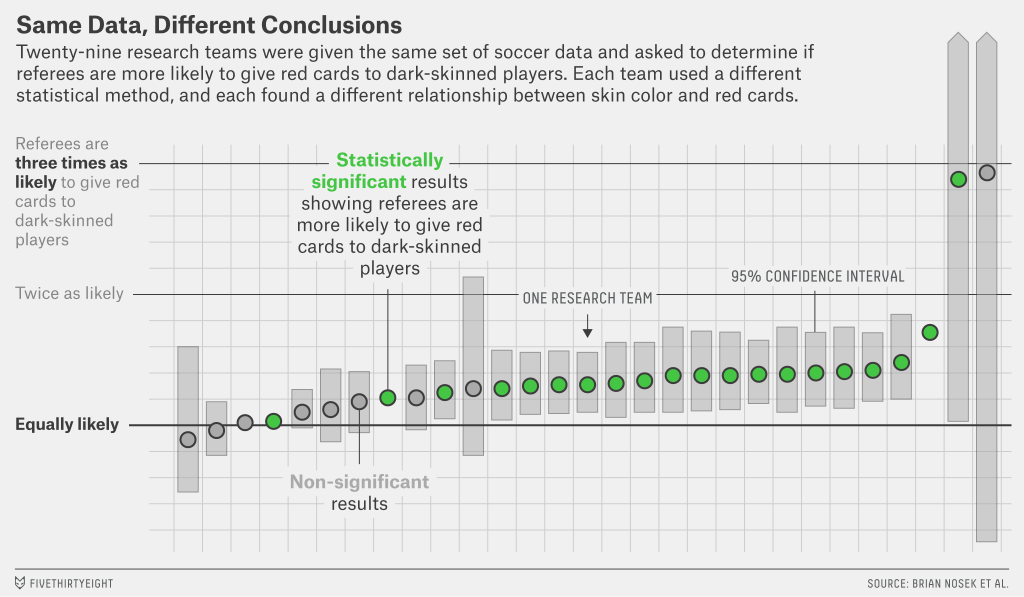
que representa lo que su leyenda reza: diversos grupos de investigación participaron en un experimento consistente en analizar independientemente un mismo conjunto de datos y tratar con él de responder si los jugadores de fútbol de color (negro, para ser más precisos) reciben proporcionalmente más tarjetas rojas que el resto.

Mismos datos, misma pregunta (o no: más sobre eso, luego), distintos métodos y diversidad de resultados. Aunque, también puede argüirse, un buen número de ellos son aproximadamente coincidentes: muestran un mediano efecto significativo.

En puridad, la pregunta a la que trataron de dar respuesta los distintos equipos no fue exactamente la misma. A la hora de concretar con precisión la hipótesis, uno puede plantear diversas variaciones y tener en cuenta (o no) distintos factores (p.e., la posición del jugador, la liga en la que juega, etc.).

Hay una discusión que se resume en lo que cuenta el párrafo anterior aquí. El gráfico está extraído de FiveThirtyEight y la discusión que lo acompaña merece también la pena: trata este y otros temas relacionados.

Finalmente, a los que os dediquéis al análisis de datos, trabajéis en consultoría o tengáis guardada en la manga una agenda normativa que impulsar, ¡enhorabuena! Fácil tenéis encontrar ese numerito menor que 0.05 que tantas puertas abre.