Mezclas de distribuciones con Stan

y <- c(rnorm(1000), rnorm(2000, 1, 0.5))

es una mezcla de dos normales (N(0, 1) y N(1, 0.5)) con pesos 1/3 y 2/3 respectivamente. Pero, ¿cómo podríamos estimar los parámetros a partir de esos datos?

Se puede usar, p.e., flexmix, que implementa eso del EM. Pero en el librillo de este maestrillo dice

library(rstan)

y <- c(rnorm(1000), rnorm(2000, 1, 0.5))

codigo <- "
data {
  int<lower=1> K; // number of mixture components
  int<lower=1> N; // number of data points
  real y[N]; // observations
}

parameters {
  simplex[K] theta; // mixing proportions
  real mu[K]; // locations of mixture components
  real<lower=0> sigma[K]; // scales of mixture components
}

model {
  real ps[K]; // temp for log component densities

  sigma ~ cauchy(0,2.5);
  mu ~ normal(0,10);

  for (n in 1:N) {
    for (k in 1:K) {
      ps[k] <- log(theta[k]) + normal_log(y[n],mu[k], sigma[k]);
    }
    increment_log_prob(log_sum_exp(ps));
  }
}"

fit <- stan(model_code = codigo,
            data = list(K = 2, N = length(y), y = y),
            iter=48000, warmup=2000,
            chains=1, thin=10)

En el código anterior no sé si queda claro cómo cada punto $latex y_i$ sigue una distribución (condicionada a los parámetros) con densidad $latex \theta_1 \phi(y_i, \mu_1, \sigma_1) + \theta_2 \phi(y_i, \mu_2, \sigma_2)$.

El resultado no es malo: los valores medianos de las muestras de los parámetros de los parámetros son próximos a los de partida, etc., como puede verse en

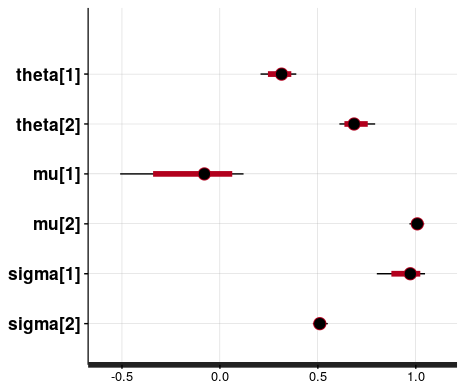
Y una coda: en la primera aproximación al problema corrí cuatro cadenas (en lugar de una sola, como en el código que comparto) y el resultado era confuso. Entre otras cosas, las distribuciones de los pesos de la mezcla eran bimodales y los intervalos de confianza muy altos. Eso se debe fundamentalmente a la no identificabilidad de los parámetros: algunas cadenas llamaban $latex \theta_1$ al peso de la normal centrada en 0 y otras a la centrada en 1. Esto puede apreciarse en el traceplot

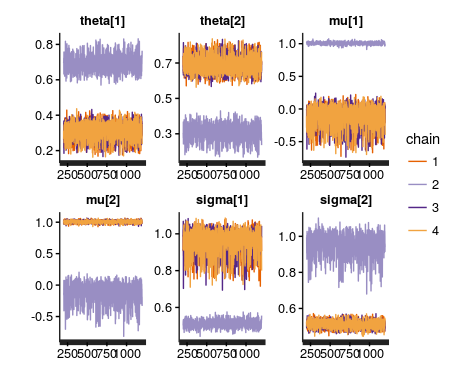
de esa primera ejecución del programa con cuatro cadenas.

Supongo que es un fenómeno conocido, aunque no he encontrado referencias al respecto en el poco tiempo que he dedicado a ello. Por eso he preferido correr una única cadena y, salvo que alguien me pueda proponer una alternativa, me parece que es lo más razonable.