El AUC es la probabilidad de que...

Voy a constuir unos datos artificiales y un modelo de clasificación binaria,

library(mgcv)
library(ggplot2)
library(pROC)

n <- 10000
dat <- gamSim(1, n=n, dist="binary", scale=.33)

lr.fit <- gam(y ~ s(x0, bs="cr") +
    s(x1, bs="cr") + s(x2, bs="cr") +
    s(x3, bs="cr"),
    family=binomial, data=dat,
    method="REML")

y luego (mal hecho: debería hacerlo sobre un conjunto de validación distinto) a obtener las predicciones para las observaciones

res <- data.frame(real = factor(dat$y),
    prob = predict(lr.fit, type = "response"))

que

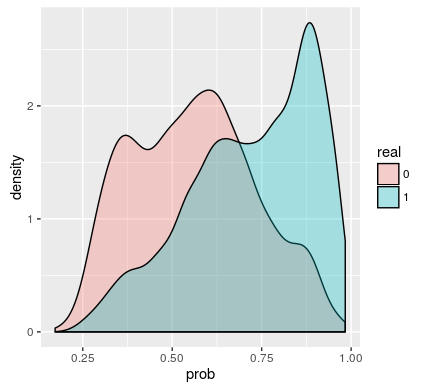
ggplot(res, aes(x=prob, fill=real)) +
    geom_density(alpha=.3)

representa así:

Me pregunto si el clasificador construido es bueno. Para lo cual voy a construir la curva ROC con

sies <- res[res$real == "1",]
noes <- res[res$real == "0",]
scores <- 0:100 / 100

q.si <- ecdf(sies$prob)(scores)
q.no <- ecdf(noes$prob)(scores)
plot(q.si, q.no, type = "l")

que produce

(Inciso: la anterior no es la curva ROC; la curva ROC tal cual la conocen casi todos es plot(1-q.no, 1-q.si, type = "l"), que es una versión simétrica de la mía).

En esta la segunda (tercera si se tiene en cuenta la del inciso) oración de la entrada, me pregunto cómo calcular el popular AUC, el área bajo esa curva (o la de la habitual, que es, en cualquier caso, la de la misma región). Puedo hacer cuadraturas, pero también puedo seleccionar puntos al azar en el cuadrado y calcular la proporción de los que caen en la zona de interés.

Muestrear el cuadrado es muestrear [0,1] uniformemente para las x por un lado y para las y por el otro. Pero las x, por ejemplo, son el rango de ecdf(sies$prob) y muestrearlo uniformemente es (de hecho, la manera canónica de) muestrear los sies$prob. Lo mismo rige para las y. Y que el punto del plano elegido al azar quede por debajo de la curva significa entonces a que el valor muestreado de sies$prob sea mayor que el de noes$prob. Así que

foo <- function(x) sample(x, 1e6, replace = TRUE)
mean(foo(sies$prob) > foo(noes$prob))

arroja no solo un valor muy similar al de pROC::roc(res$real, res$prob)$auc sino que, además, proporciona una interpretación interesante de este indicador: el AUC es la probabilidad de que, tomados un caso positivo y uno negativo al azar, el scoring del modelo para el primero sea superior al segundo.