Polinomios monótonos
Recibí un mensaje el otro día sobre polinomios monótonos. Mejor dicho, sobre el ajuste de datos usando polinomios monótonos. Frente a un modelo del tipo y ~ x (x e y reales) donde la relación entre las dos variables es
- manifiestamente no lineal y
- necesariamente monótina, p.e., creciente (por consideraciones previas),
cabe considerar ajustar un polinomio monótono, i.e., realizar una regresión polinómica con la restricción adicional de que el polinomio de ajuste resultante sea monótono.
¿Cómo? Así. En el artículo se describe un procedimiento, implementado luego en el paquete MonoPoly de R, que se basa en una caracterización de la condición de monotonía para polinomios. Por ejemplo, que un polinomio de orden par monótono en el intervalo $latex [a,b]$ tiene que ser la integral indefinida de otro de la forma
$$ p_1(x)^2 + (x-a)(b-x) p_2(x)^2$$
El resto del artículo se sigue de esa parametrización por las vías previsibles. Paz y después, gloria.
Pero, ¿son necesarios polinomios de grado 9 o 15 para ajustar modelos como los que siguen?
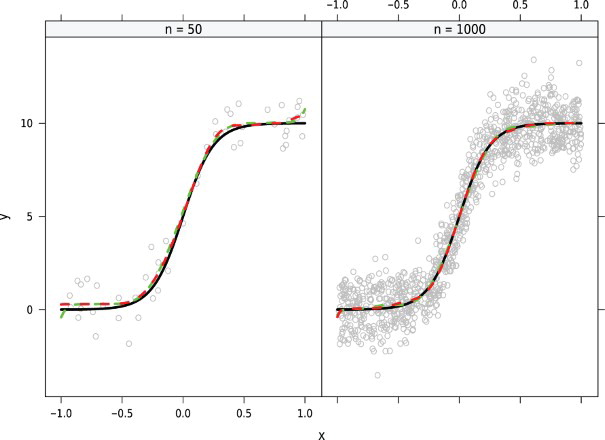
El artículo no está mal, no miente, pero podríamos pensar que engaña: ¿por qué seguir la vía de incrementar el orden de los polinomios en lugar de utilizar splines? ¿Por qué no proponer al lector el uso de splines monótonos?
