Calibración de probabilidades vía apuestas
Después de la remontada del F.C. Barcelona es muy de agradecer ver la publicación de artículos como Cómo de improbable era la remontada del Barcelona de Kiko Llaneras. En la misma entradilla, indica que [u]n modelo estadístico y las apuestas le daban el 7% de opciones. Un 7% viene a ser más o menos, dice correctamente, como sacar un 11 o un 12 en una tirada de dos dados.
La pregunta que podemos hacernos, de todos modos, es si las probabilidades estimadas por esos modelos estadísticos o las casas de apuestas están o no bien calibradas. Es decir, si, por ejemplo, el número de aciertos para eventos con una probabilidad asignada del alrededor del 0.25 es o no próximo al 25%.
Para el modelo estadístico al que se refiere el artículo, no creo que podamos decir gran cosa: no tenemos casi seguro suficiente información histórica. Sin embargo, una paseo rápido por Google nos conduce a una serie de artículos como este o este, en los que se estudia el asunto.
Del primero extraigo el gráfico
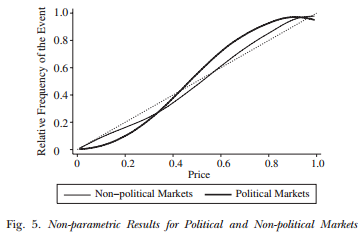
que muestra la descalibración entre las frecuencias reales (eje vertical) y las probabilidades deducidas de los precios (eje horizontal). La calibración es particularmente mala para los eventos de índole política: a ojo, un poco menos del 10% de los eventos a la que las apuestas asignaron una probabilidad del 20% ocurrieron; y ocurrieron más del 80% de los eventos a las que las apuestas daban una probabilidad del 70%. Las probabilidades para los eventos no políticos parecen estar mejor ajustadas.
La calidad de la calibración depende también (¡obviamente!) del tiempo hasta que sucede el evento:
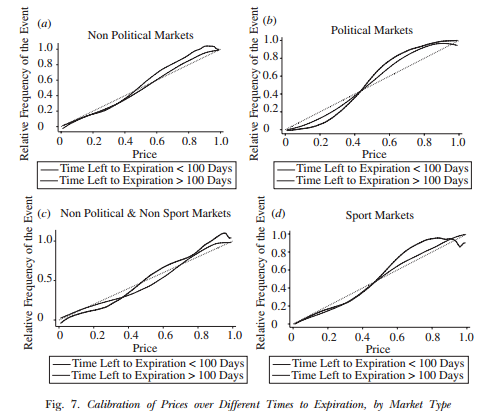
Así que, en resumen, parece que habría cierta confianza en que esa probabilidad asignada por las casas de apuestas podría ser una buena guía en este caso.
Y acabo con una nota para los lectores habituales del blog que es una advertencia para que no lo tomen demasiado en serio. Si se recuerdan ocho partidos en competiciones europeas con un resultado en el partido de ida de 4-0 y nunca se ha visto una remontada, la estimación de la probabilidad que podrían haber hecho es 3/8 (37%). Después de observar la remontada, podrían actualizarla a 1/9 (11%); pero si hubiese pasado lo contrario, se habría actualizado a 3/9, ¡tres veces más!
