¿Les dará un patatús a mis excolegas?
En Gaussianos publicaron este problema:
En un triángulo acutángulo ABC tenemos que AH, AD y AM son, respectivamente, la altura, la bisectriz y la mediana que parten desde A, estando H, D y M en el lado BC. Si las longitudes de AB, AC y MD son, respectivamente, 11, 8 y 1, calcula la longitud del segmento DH.
El gráfico, construido por uno de los respondedores, Ignacio Larrosa Cañestro, es este: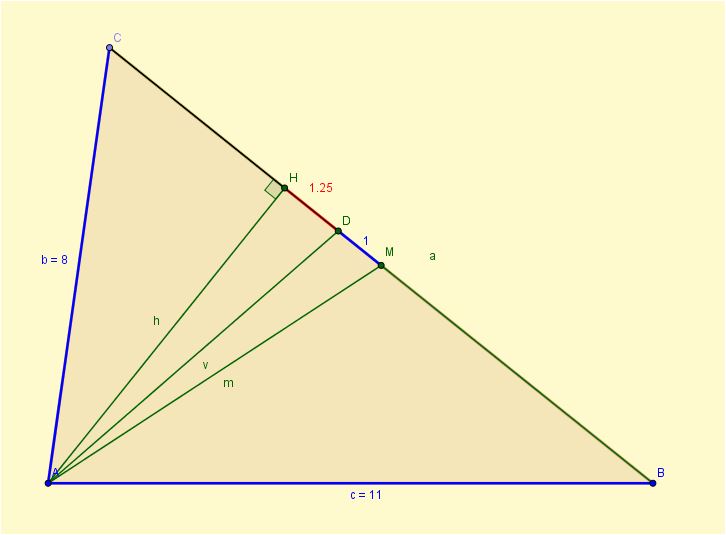
Mi solución (puro uso del teorema del seno):
library(nleqslv)
ab <- 11
ac <- 8
foo <- function(abc, print.answer = FALSE){
acb <- asin(sin(abc) * ab / ac)
bac <- pi - acb - abc
bc <- ab * sin(bac) / sin(acb) # lado opuesto
bad <- bac / 2
adb <- pi - bad - abc
base.bisectriz <- ab * sin(bad) / sin(adb)
base.mediana <- bc / 2
base.altura <- ab * cos(abc)
if (print.answer)
return(abs(base.altura - base.bisectriz))
delta <- abs(base.mediana - base.bisectriz)
}
z <- nleqslv(0.5, function(abc) foo(abc) - 1)
foo(z$x, print.answer = T)A ver qué dicen.

