Sigo con ajustes robustos. Y cosas que como matemático, me ponen muy nervioso.
Una de las maneras de hacer ajustes robustos es la de sustituir la función cuadrática por la biweight. Es decir, utilizar la función que aparece la derecha en
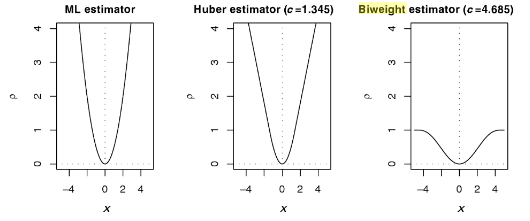
en lugar de la de la izquierda. O, dicho de otra manera, en lugar de tratar de minimizar
$$ \sum_i \rho(y_i - f_\alpha(x_i))$$
usando $\rho(x) = x^2$, que es la función que se representa a la izquierda y a la que estamos acostumbrados, usar la de la derecha. Que es la función biweight de Tukey.
Pero esa función es plana a una determinada distancia de cero. Es decir, utilizar esa función es utilizar una función que tiene _mínimos locales _por doquier (y que son iguales a su máximo absoluto, dicho sea de paso). Que es lo más parecido de dispararse en el pie antes en la línea de salida de la maratón.
Obviamente, una implementación satisfactoria del problema de minimización necesita valores iniciales razonables. Que ojalá estuviesen siempre a mano.
En fin.
Nota final: No hay secta más hermética que la de la gente que se dedica a los ajustes robustos. Creo que lo hacen a propósito para darse importancia.