Distancias (I): el planteamiento del problema
Me han pedido (vía Twitter) que desarrolle cosas que tengo por ahí desperdigadas (p.e., en las notas de esos cursos que ya no daré y puede que en algunas entradas viejunas de este blog) sobre distancias.
¿Por qué son importantes las distancias? Por un principio que no suele ser explicitado tanto como merece en ciencia de datos: si quieres saber algo sobre un sujeto, busca unos cuantos parecidos y razona sobre ellos.
¿Algunos ejemplos del uso de distancias en ciencia de datos? P.e., al aplicar técnicas de clústering, en los (muy habitualmente infraestimados) k-vecinos. Aunque también en lugares insospechados (corolarios del principio enunciado en el párrafo anterior) tales como este, donde para medir la bondad de, explicar y entender una predicción (construida con cualquier tipo de modelo), sugieren crear gráficos tales como
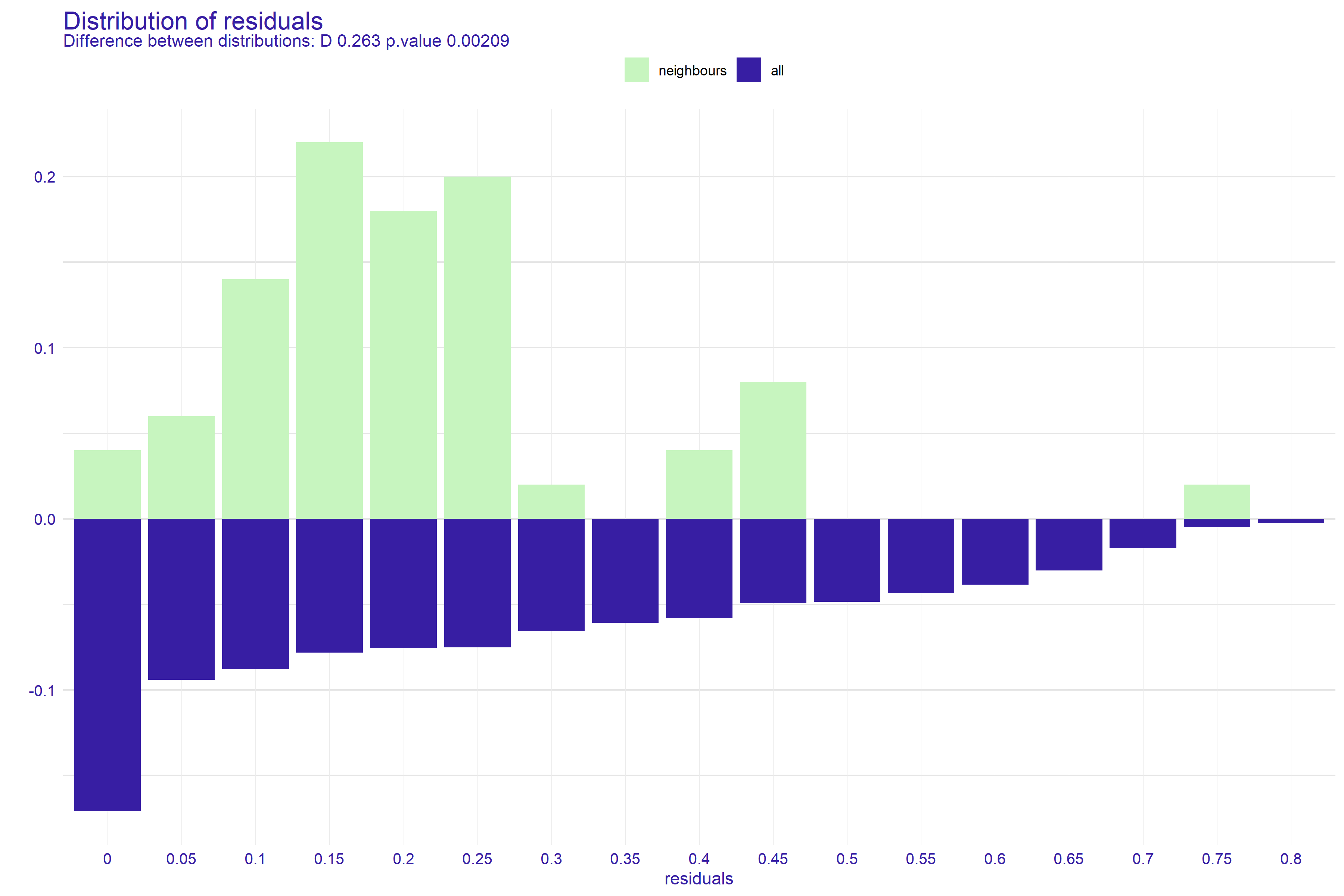
donde se compara de cierta manera (que no ha lugar desarrollar aquí) la observación de interés con sus 50 vecinos.
¿Dónde radica el principal problema del uso de distancias en ciencia de datos? Sin duda ninguna, en cómo se enseña el asunto, que no tiene prácticamente nada que ver con cómo emerge luego en las aplicaciones. No hay fuente que conozca que no introduzca el asunto usando puntos en el plano (y usando la distancia euclídea) y pocos van algo más allá.
Ese caso de uso tiene cierto interés en algún tipo de aplicaciones (con imágenes, supongo) no centrales en lo que suele consistir la práctica de la ciencia de datos. Por dos motivos relacionados:
- Porque las/esas distancias son distancias (matemáticas).
- Por la homogeneidad (y más: invariancia frente a rotaciones, traslaciones, etc.) de ese tipo de datos.
Dejo el asunto aquí y en una siguiente entrada trataré el asunto de por qué las distancias (que encontramos en la práctica) no son distancias (de las que nos hablan los libros).
