Más sobre aquel concepto estadístico que aconsejé desaprender: la suficiencia

En esta entrada abundo en una que escribí hace ocho años: Conceptos estadísticos que desaprender: la suficiencia. Lo hago porque casualmente he tropezado con su origen y justificación primera, el afamado artículo On the Mathematical Foundations of Theoretical Statistics del nunca suficientemente encarecido R.A. Fisher.

Criticaba en su día lo inútil del concepto. Al menos, en la práctica moderna de la estadística: para ninguno de los conjuntos de datos para los que trabajo existe un estadístico suficiente que no sea la totalidad de los datos.

Entonces, ¿por qué la suficiencia? Escuchemos (leamos) lo que Fisher tiene a bien decirnos. En primer lugar, sobre lo que la estadística es y —aunque viene a ser lo mismo— para lo que sirve:

Obviamente, discrepo —aunque dejo la crítica para otra ocasión—, pero se le abona a Fisher la claridad. Más adelante, Fisher enumera ls tres subproblemas asociados a la reducción de los datos:

Es muy interesante lo que tiene que decir Fisher sobre (1). Por ejemplo, que no queda más remedio que limitarse a distribuciones que estén previamente tabuladas (¡servidumbres de la época!), pero lo relevante para la entrada de hoy tiene que ver con (2): la construcción de estimadores.

A estos les exige consistencia, que viene a decir que deberían converger al valor real conforme se incrementase el tamaño de la muestra.También le preocupa la eficiencia, sobre la que lo que tiene que decir es fabuloso e invito al lector a consultarlo: lo encontrará en los dos primeros párrafos de la cuarta sección.

Pero también menciona otro criterio, el de la suficiencia:

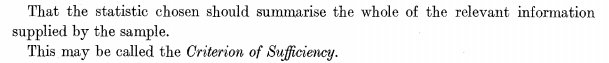
y lo enlaza con la eficiencia a través de la enunciación implícita de un teorema que adorna los libros modernos de estadística viejuna, el que relaciona suficiencia con eficiencia.

El criterio de suficiencia, como se ve, nació en un contexto muy particular, desde la perspectiva y la experiencia en una serie de problemas estadísticos muy concretos y alejados del quehacer de muchos estadísticos hoy en día y que, por algún motivo, aún encuentra acomodo en los programas de estadística contemporáneos. Como tal, es totalmente inútil.

Pero es rescatable, lo admito, como un caso particular de un folk theorem (por folk theorem me refiero a un resultado que nunca ha sido formulado ni demostrado formalmente pero que todo el mundo usa y conoce) que viene a decir que a la hora de construir modelos es importante incorporar toda la información posible. Como he leído alguna vez por ahí, si no lo haces, te dejas dinero encima de la mesa. En algunos casos muy concretos se dispone de estadísticos suficientes que, por definición, contienen toda la información disponible en los datos. Pero la suficiencia debería verse como un extremo irreal e inalcanzable en un continuo, la cantidad de información de la que dispone el modelo, para mejorar su eficiencia.