La probabilidad de que 2+2 siga siendo 4 dentro de 12 meses es algo menor del 100%
Escribí hace un tiempo sobre las probabilidades subjetivas y cómo Leonard Savage sugería pensar en la probabilidad de un evento como
la [máxima] cantidad que uno debería estar dispuesto a pagar por el derecho a recibir 100 € si el evento finalmente ocurre.
De acuerdo con esa definición, ¿cuál sería la probabilidad de que 2+2 siga siendo 4 dentro de doce meses? Uno estaría tentado a decir que es del 100%, es decir, que pagaría hasta 100 € por el derecho a recibir 100 € en un año si 2+2 es todavía 4 para entonces.
Pero para pagar 100 € ahora, tendría que vender 100 € del fondo monetario en el que uno guarda el dinero y que da el 2% (largo) anual. Así que uno perdería el interés correspondiente los siguientes 12 meses. De manera que hoy uno estaría dispuesto a pagar no más de unos 98 €. El motivo no son dudas sobre la persistencia de las reglas de la aritmética sino los tipos de interés (y la relación entre el valor del dinero hoy y el valor del dinero mañana).
Así ha de entenderse el mercado de Polymarket
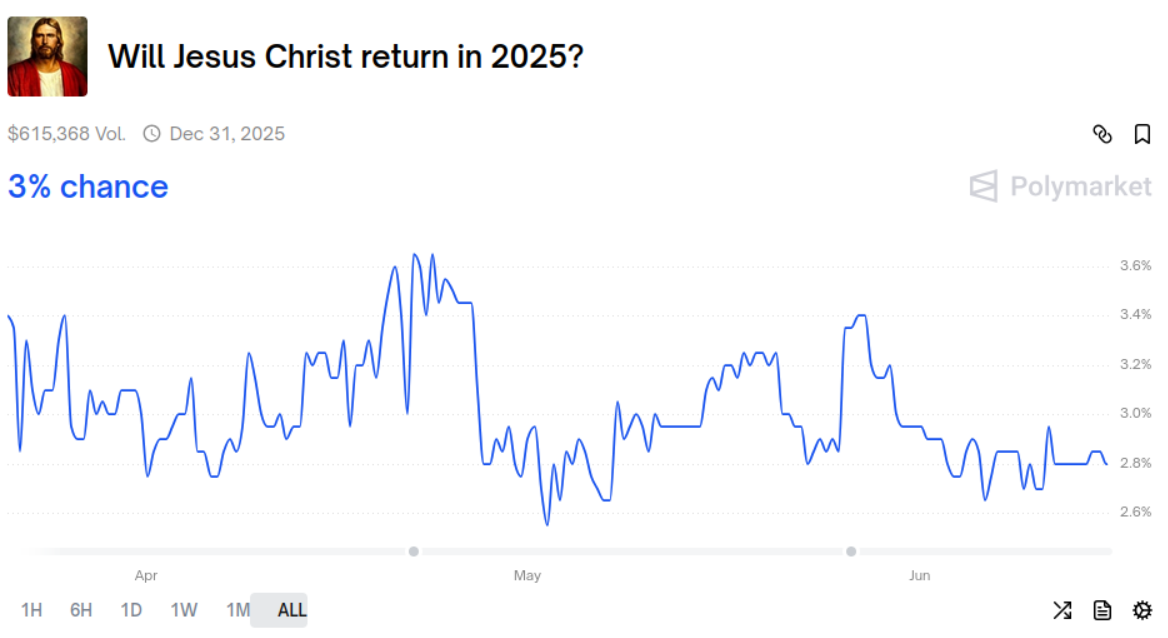
que, casi seguro, refleja más el efecto de los tipos de interés en EEUU (en Polymarket se opera con una stablecoin que sigue al dólar) que cualquier otra cosa.
Una nota final
Días después de escrita esta entrada, publicó Robin Hanson otra en el suyo, esta, en la que trataba un asunto relacionado: cómo en los mercados de apuestas como los tratados arriba se tiende a infraponderar la probabilidad de los eventos más probables. El motivo es que apostar por ellos implica un desembolso grande ahora.
