"Intervalos" de confianza con forma de rosquilla

Envalentonado por el comentario de Iñaki Úcar a mi entrada del otro día, que me remitía a este artículo, decidí rizar el rizo y crear intervalos de confianza no ya discontinuos sino con otra propiedad topológica imposible: homeomorfos con un toro.

Y aquí está:

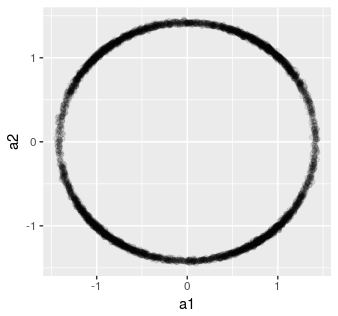
El modelo, el código y demás,

library(rstan)
library(ggplot2)

n <- 100

a1 <- 1
a2 <- 1
sigma <- 0.4

datos <- data.frame(x1 = rnorm(n, 2, 0.1),
                    x2 = rnorm(n, 2, 0.1))

datos$y <- a1^datos$x1 + a2^datos$x2 + rnorm(n, 0, sigma)

codigo <- "
data {
  int<lower=1> N;
  real y[N];
  real x1[N];
  real x2[N];
}

parameters {
  real<lower=-3, upper="3"> a1;
  real<lower=-3, upper="3"> a2;
  real<lower=0, upper="3"> sigma;
}

model {
  for (n in 1:N)
    y[n] ~ normal(fabs(a1)^x1[n] +
      fabs(a2)^x2[n], sigma);
}"

fit <- stan(model_code = codigo,
    data = list(N = length(datos$y), y = datos$y,
                x1 = datos$x1, x2 = datos$x2),
    iter=40000, warmup=2000,
    chains=1, thin=10)

res <- as.data.frame(fit)

ggplot(res, aes(x = a1, y = a2)) + geom_point(alpha = 0.1)

De nuevo, no son intervalos propiamente dichos, lo convengo. Pero son configuraciones más fieles al espíritu de lo que un intervalo de confianza es y representa que su(s) letra(s) I N T E R V A L O.

¿Y la parte seria? Hoy la hay y es que en algunos modelos (¿mal especificados?) puede existir un problema de indeterminación de coeficientes. Por ejemplo, si en una regresión lineal hay dos predictores demasiado correlados, las posterioris de sus coeficientes vivirán en una región apepinada del espacio. Que degenerará en una recta cuando los coeficientes sean idénticos.

En este ejemplo tonto, existe una artificial indeterminación angular, si se me permite, de los coeficientes.