Sobre sumas de cuadrados de normales con varianzas desiguales

En mi entrada anterior mencioné cómo la suma de cuadrados de normales, aun cuando tengan varianzas desiguales, sigue siendo aproximadamente $latex \chi^2$. Es el resultado que subyace, por ejemplo, a la aproximación de Welch que usa R por defecto en t.test. Puede verse una discusión teórica sobre el asunto así como enlaces a la literatura relevante aquí.

Esta entrada es un complemento a la anterior que tiene lo que a la otra le faltan: gráficos. Al fin y al cabo, es un resultado que se prueba a ojo: efectivamente, la suma de […] tiene aspecto de $latex \chi^2$, determinemos su parámetro.

La entrada tiene tres partes en la que se examinará tres casos de creciente grado de generalidad: el teórico/conocido, aquél en el que las varianzas son iguales aunque distintas de 1 y, finalmente, el general de varianzas desiguales.

I.

El caso conocido de todos está ilustrado por

n <- 10
muestra <- replicate(10000, {
  muestra <- rnorm(n, 0, 1)
  res <- sum(muestra^2)
})

hist(muestra, breaks = 100,
      freq = F, main = "ajuste de la X²")
curve(dchisq(x, n), 0,
      max(muestra), add = T, col = "red")

que produce

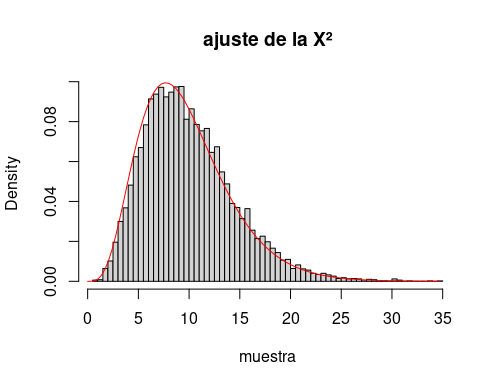
El código genera n variables aleatorias normales estándar, las eleva al cuadrado, las suma, construye su histograma y lo compara con la densidad de la $latex \chi^2$ de n grados de libertad.

II.

El caso de varianzas distintas se reduce al anterior dividiendo la muestra por dicha varianza. Eso sí, hay que tener en cuenta que no es la suma de los cuadrados la que tiene distribución $latex \chi^2$ sino esta dividida por la varianza de cada una de las normales (o su varianza media, como se verá luego):

n <- 10
sds <- 1.5

muestra <- replicate(10000, {
  muestra <- rnorm(n, 0, sds)
  res <- sum(muestra^2)
})

muestra <- muestra / sds^2

hist(muestra, breaks = 100,
      freq = F, main = "ajuste de la X²")
curve(dchisq(x, res$maximum), 0,
      max(muestra), add = T, col = "red")

Que produce

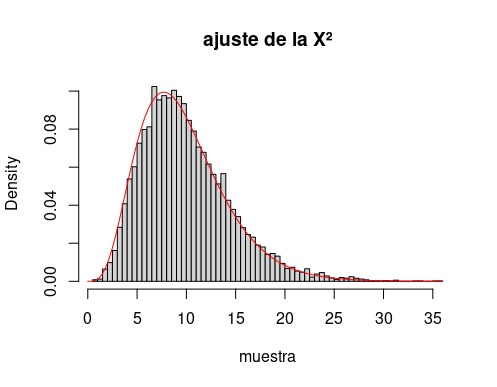
III.

En esta tercera parte se van a sumar cuadrados de variables aleatorias normales con varianzas desiguales:

set.seed(2021)

n <- 10

sds <- exp(rnorm(n, .1, .5))
#sds <- rep(2, 10)

muestra <- replicate(10000, {
  muestra <- sapply(sds, function(sd) rnorm(1, 0, sd))
  res <- sum(muestra^2)
})

hist(muestra, breaks = 100,
      freq = F, main = "¿parece X²?")

Con lo que se obtiene

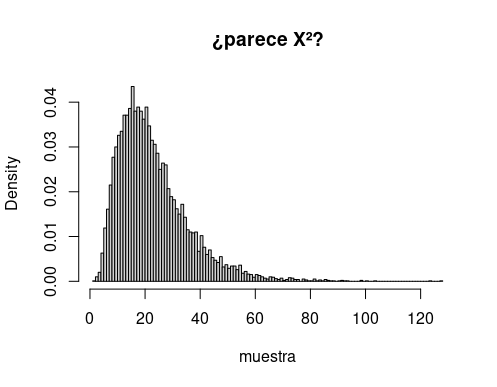
Obviamente, el soporte de ese histograma va a depender críticamente de la varianza de las observaciones, por lo que, extendiendo la corrección de la sección anterior, se escala

muestra <- muestra / mean(sds^2)

de manera que el resultado sigue pareciendo a ojo $latex \chi^2$. Pero, ¿con qué parámetro? Los enlaces con los que se abría esta entrada sugieren utilizar el método de los momentos, que equivaldría a tomar un número de grados de libertad igual la media de muestra.

Pero en este blog somos gente de orden y la programación no nos es ajena. Por eso vamos a tratar de maximizar la verosimilitud:

foo <- function(nu)
  sum(dchisq(muestra, nu, log = TRUE))

res <- optimize(foo,
  interval = c(6, 100),
  maximum = TRUE)

hist(muestra, breaks = 100, freq = F)
curve(dchisq(x, res$maximum), 0, max(muestra),
    add = T, col = "red")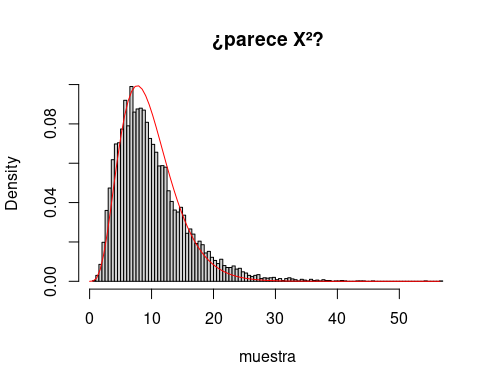

Bueno, bien, vale, aceptamos barco. Es, efectivamente, la aproximación que se merecen los que aplican el t.test con varianzas desiguales.