¿Cuántas iteraciones necesita mi MCMC?

Es el tema de este reciente artículo de Gelman. Cabe esperar que algunos se sientan decepcionados porque no tenga solo una página en la que se lea algo así como: usa cuatro cadenas de 4000 iteraciones, 1000 de ellas de warmup. Lo siento: son 26 páginas y sin recetas copy-paste.

Tampoco puedo añadir nada de sustancia a lo que ahí se cuenta. Me voy a limitar a subrayar una idea e ilustrarla con un caso con el que me enfrenté hace unos años.

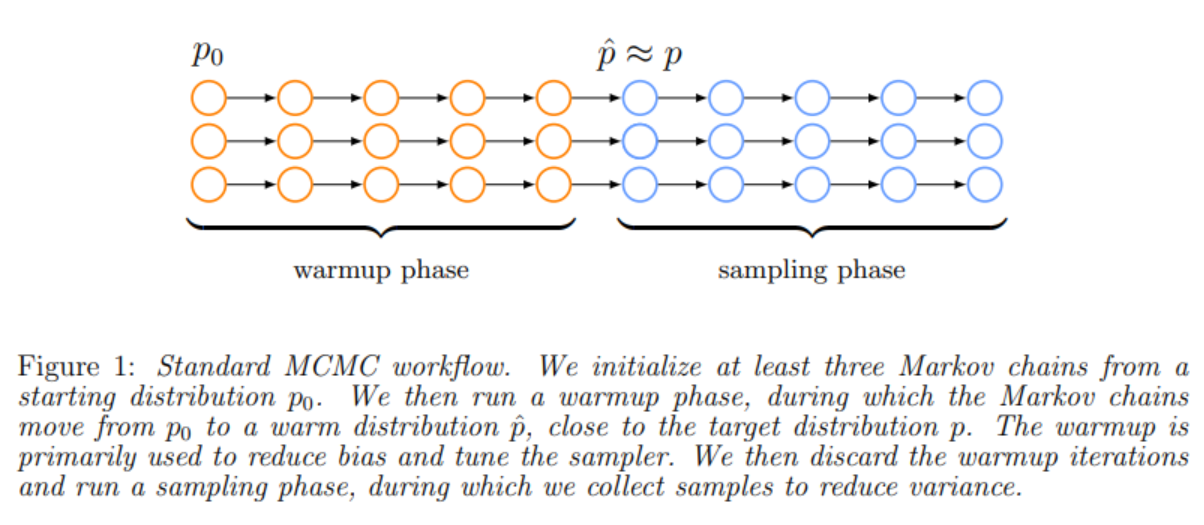
Como se indica en el artículo e ilustra la gráfica anterior, uno lanza varias cadenas que tienen dos fases diferenciadas: calentamiento y muestreo propiamente dicho. Los parámetros iniciales de la distribución de la cadena pueden estar muy alejados de los reales y el calentamiento puede interpretarse casi como una optimización. De hecho, si uno busca en Google mcmc fucntion optimization encuentra resultados relacionados con el asunto. MCMC no está pensado para eso y no es óptimo, pero aun así, puede usarse para obtener valores próximos a un máximo o mínimo.

Muchos problemas de optimización son sencillos. Encontrar los parámetros de la mejor recta que blablablá (la regresión lineal) es un problema de optimización muy simple. Cabe esperar que, independientemente de lo alejados que estén los parámetros iniciales de los óptimos, el calentamiento propiamente dicho del MCMC para ajustar el modelo sea breve: enseguida comenzará a muestrear cerca del óptimo.

Hace unos años, sin embargo, estaba trabajando en un problema similar pero más complejo: no tenía una regresión lineal sino no lineal. El mínimo estaba en una especie de valle estrecho con forma aplatanada rodeada de mesetas. Los métodos de optimización tradicionales sufrían para ubicar ese punto feliz. El problema de la optimización determinista, en todo caso, era que no aportaba apenas información sobre el error estándar de los parámetros —o, más en general, la densidad de la posteriori—. Así que intenté —y logré parcialmente— reescribir bayesianamente todo el proceso de ajuste.

¿Qué ocurría con el calentamiento? Algo parecido a esto:

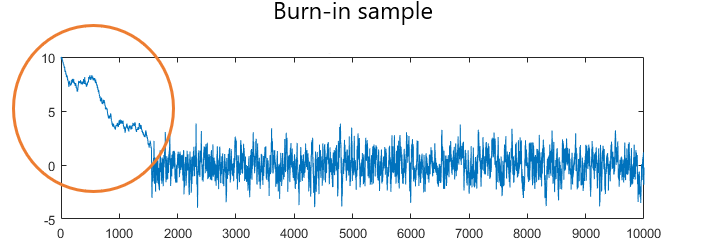
Con dos diferencias:

• Tenía muchos más parámetros, no solo uno.
• La convergencia durante el calentamiento era muchísimo más lenta.

No estaba nunca claro cómo preestablecer la longitud del calentamiento: dependía mucho de cada caso. Dependiendo de los datos concretos, la optimización era solo complicada o llegaba a ser endemoniada y la cadena renqueaba hacia el mínimo a través de miles de iteraciones.

Y termino con una carta para los reyes magos: este año quiero que me traigan un software para el ajuste de modelos vía MCMC que identifique razonablemente bien cuándo ha comenzado el calentamiento y que comience el muestreo por su cuenta sin necesidad de utilizar valores fijos preespecificados.