Pues los SVMs, al final, no son tan exóticos

Impartí un curso sobre máquinas de vector soporte (SVMs en lo que sigue) en Lima el pasado mes de agosto.

Las SVMs (o más propiamente, los clasificadores de margen máximo) son exóticos dentro del repertorio del científico de datos. Lo que buscan es un hiperplano que maximiza el margen entre tirios o troyanos,

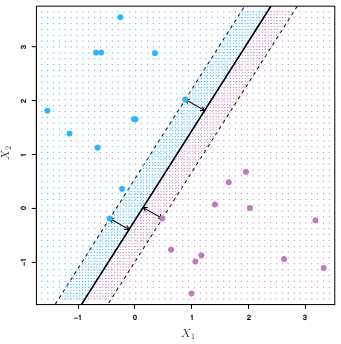
con o sin penalización para los puntos que insisten en permanecer en la región del espacio que no les corresponde. El modelo se ajusta resolviendo un problema de minimización inhabitual: uno de los llamados programas cuadráticos convexos. (Del que no nos tenemos que preocupar habitualmente porque delegamos la resolución en el software).

Sin embargo, preparando el material, vine a tropezar con una reformulación del problema anterior, que lo reduce a la minimización de una función de pérdida particular. En efecto, en la sección 12.3.2 del archiconocido ESL se plantea cómo en el contexto habitual de la clasificación (penalizada)

$$ \min \sum_1^N L(y_i, f(x_i)) + \frac{\lambda}{2} |\beta|^2,$$

donde $latex f(x) = h(x) \beta + \beta_0$, se obtiene

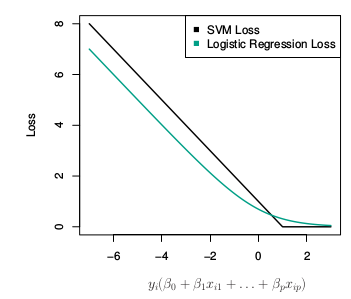
• la regresión logística (penalizada) si $latex L(y, x) = \log(1 + \exp(-yf(x))$ y
• SVM cuando $latex L(y, x) = [1 - yf(x)]+$ (donde $latex [x]+$ representa la parte positiva de $latex x$).

Resumiendo, en el fondo, estamos haciendo, casi, regresión logística (con o sin kernels, dependiendo de $latex h$) dado que las dos funciones de pérdida son, geométricamente, bastante parecidas:

Comentarios:

• Me encantan los resultados que subsumen unas cosas en otras.
• Busqué y no encontré referencias a cuándo fue y de mano de quién que vino a obtenerse esta reformulación. ¿Será del mismo Vapnik? ¿Será de otro? ¿Será esta? ¿Le sabría malo?
• Es posible ajustar modelos SVM sin tener que plantear un programa cuadrático, etc. Basta con minimizar la función de pérdida anterior directamente, como hace el paquete gcdnet de R.