Medias ponderadas a lo Uluru

Dicen que el brote de inflación que estamos viviendo es atípico (y según algunos, menos preocupante) porque no está generalizada sino concentrada en un número pequeño de productos.

Trae The Economist en su número del 6 de noviembre (de 2021) un artículo al respecto que tiene cierto interés estadístico. Comienza comparando la inflación de ahora con la de otros años donde el incremento de los precios fue, de acuerdo con cómo se computa tradicionalmente la inflación, igual, a través de la distribución de los incrementos de precios sobre las distintas categorías:

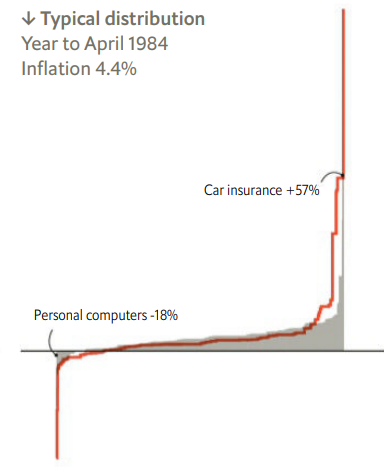
En gris aparecen los incrementos de precios de las distintas categorías de productos en 1984 (¡gran año!) ordenadas de menor a mayor y sobre ella se muestran, en rojo, las de 2021. Se aprecia cómo la subida de precios de 1984 fue más sistemática, a través de toda la distribución, mientras que la de 2021 se concentra más en la cola de la derecha (o más propiamente, en una serie de productos anómalos).

La pregunta que se formula The Economist para el caso concreto de la inflación y que nos podemos plantear más generalmente en estadística es: ¿cómo resumir esa distribución entera en una única cifra que tenga sentido? (Lo cual debería comenzar resolviendo qué significa tener sentido, obviamente.)

Los gráficos con los que The Economist acompaña la discusión subsiguiente deberían ser rescatados para muchos manuales introductorios. Comienza con cómo se calcula actualmente la inflación por antonomasia:

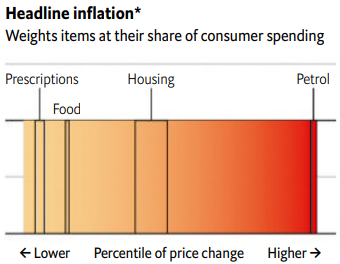
En ella, las distintas categorías de productos están distribuidas sobre el eje horizontal de menor (amarillo) a mayor (rojo) incrementos de precios. El eje vertical indica el peso que tienen en el índice global.

[Nota: realmente, se usa una doble ponderación: existe una previa que consiste en el tamaño que tienen las distintas categorías de productos en la cesta familiar. Pero creo que eso ya es bien sabido de todos y que no merece abundamiento.]

Luego, muestra cómo se calcula la llamada inflación subyacente:

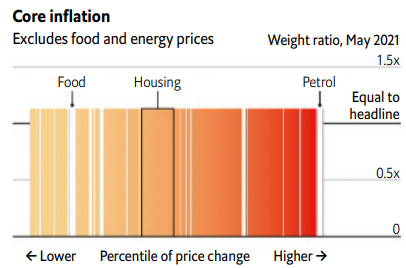
Es lo mismo, solo que el peso de algunas categorías de productos ha sido reducido a cero. (No vamos a entrar aquí en los motivos: está más que bien explicado en muchas otras partes.)

La novedad consiste en usar medias recortadas, como se ve que ha propuesto algún organismo. En concreto, asignando pesos de la siguiente manera:

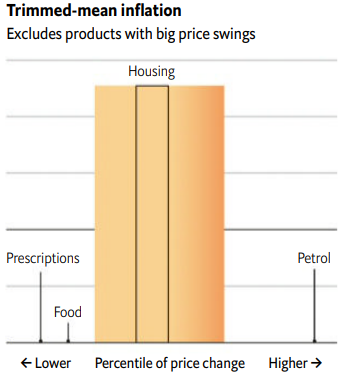
Es decir, no sacando del índice ciertas categorías preestablecidas de productos sino precisamente aquellas que están en la cola de la distribución, sean ellas las que sean en cada periodo.

Finalmente, la propuesta de The Economist consiste en usar pesos Uluru, es decir,

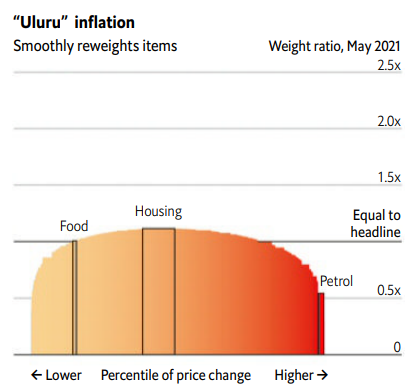
que es una versión suave de lo anterior con la que la publicación hace sus pinitos en el mundo de la estadística robusta con una propuesta de lo más colorida.

[Porque, a todo esto, Uluru es un cerro de Australia rodeado de aborígenes alcoholizados y de mal cariz al que, a falta, de nada mejor en aquel islote estéril, inducen a los turistas a visitar.]

A continuación, mis comentarios.

Este es un capítulo más en un viejo tipo de debate —convertido ya casi en un subgénero literario propio— que consiste en discutir sobre el indicador numérico más conveniente para resumir una distribución de probabilidad. Siempre tiene esta estructura: alguien propone un número (p.e., la media, o la media winsorizada, o…) consciente de sus ventajas e inconvenientes. Luego, la gente lo critica y propone otro ad hoc, etc. y la historia continua. Pero cuando uno pisa la pelota y plantea la conversación es enteramente circular porque no existe un solo indicador numérico que pueda recoger todas las peculiaridades interesantes de una distribución, todos lo miran como si fuese un marciano (y luego siguen con lo suyo).

Quiero además añadir algo sobre una discusión a la que solo he apuntado más arriba (y que The Economist trata solo implícitamente): ¿qué haría que un indicador tuviese sentido? En este contexto, vendría a ser algo así como que no generase falsos positivos. La gente ve un pico en el IPC y piensa: se nos viene la inflación, como en los setenta o los ochenta. Entonces, los (o ciertos) economistas se sienten obligados a escribir artículos explicando cómo aunque el incremento del IPC de hogaño es nominalmente similar al de antaño, el fenómeno económico subyacente es distinto porque blablablá (véase el enlace del primer párrafo de la entrada como ejemplo de esta neoliteratura). Querríase pues un indicador que no mostrase un pico si efectivamente estamos viviendo un episodio puntual de precios anómalos y que solo se disparase de existir una subida generalizada de precios con vocación de permanencia. Lo que, además, haría innecesarias las aclaraciones. (Aunque generaría otro tipo de literatura: el de los economistas heterodoxos que publicarían por ahí cómo aunque la inflación a lo Uluru dice una cosa para mantener sujeto al personal, la inflación calculada como toda la vida de Dios es el quinto caballo del Apocalipsis.)

Y una última nota. La inflación tradicional y la subyacente son, en el fondo, operadores lineales. Así, la inflación calculada sobre dos periodos sucesivos coincidiría con la combinación de las inflaciones calculadas sobre cada subperiodo independientemente. Pero no así con las recortadas, winsorizadas, ulurizadas, etc., que implica realizar operaciones no lineales sobre la distribución de los subcomponentes.